题目内容
对正整数n,设抛物线y2=2(2n+1)x,过P(2n,0)任作直线l交抛物线于An,Bn两点,则数列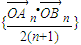 的前n项和公式是 .
的前n项和公式是 .
【答案】分析:设An(xn1,yn1),B(xn2,yn2),直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,求出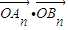 的表达式,然后利用韦达定理代入得
的表达式,然后利用韦达定理代入得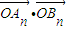 =-4n2-4n,故可得
=-4n2-4n,故可得 ,据此可得数列
,据此可得数列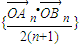 的前n项和.
的前n项和.
解答:解:设直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,
设An(xn1,yn1),B(xn2,yn2),
则 ,
,
用韦达定理代入得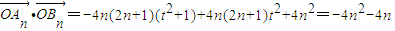 ,
,
故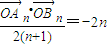 ,
,
故数列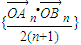 的前n项和-n(n+1),
的前n项和-n(n+1),
故答案为-n(n+1).
点评:本题主要考查直线与圆锥曲线的综合问题的知识点,向量与圆锥曲线,数列结合时,一般使用向量的坐标运算与方程的根联系起来,从而转化为根与系数的关系.这是处理向量与圆锥曲线综合问题的基本思路.
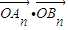 的表达式,然后利用韦达定理代入得
的表达式,然后利用韦达定理代入得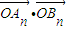 =-4n2-4n,故可得
=-4n2-4n,故可得 ,据此可得数列
,据此可得数列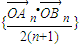 的前n项和.
的前n项和.解答:解:设直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,
设An(xn1,yn1),B(xn2,yn2),
则
 ,
,用韦达定理代入得
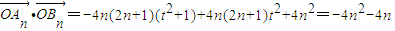 ,
,故
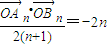 ,
,故数列
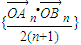 的前n项和-n(n+1),
的前n项和-n(n+1),故答案为-n(n+1).
点评:本题主要考查直线与圆锥曲线的综合问题的知识点,向量与圆锥曲线,数列结合时,一般使用向量的坐标运算与方程的根联系起来,从而转化为根与系数的关系.这是处理向量与圆锥曲线综合问题的基本思路.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
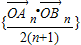 的前n项和公式是 .
的前n项和公式是 .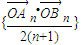 的前n项和公式是 .
的前n项和公式是 . 的前n项和公式是 .
的前n项和公式是 .