题目内容
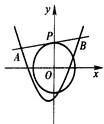 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.(1)当k=-2,m=-1,n=-1时,判断△OAB的形状;
(2)△OAB是以AB为底的等腰三角形;
①试求出P点纵坐标n满足的等量关系;
②若将①中的等量关系右边化为零,左边关于n的代数式可表为(n+1)2(ax2+bx+c)的形式,且满足条件的等腰三角形有3个,求k的取值范围.
分析:(1)根据k=-2,m=-1,n=-1,以及切线l:-x-y=2,分别得到一个等式,通过两个等式联立解方程组求出两组解,此时即可表示出两个点A,B的坐标,然后分别根据
•
=0,|
|=|
|=2.垂直与腰相等两个关系判断出△OAB是等腰直角三角形
(2) ①写出过P的切线,然后分别设出A,B两个点的坐标.根据是已知题意列出3个等式,然后解出结果..通过P点纵坐标为n,代入P中求出n的等量关系.
②按照①的结果,通过把等量关系右边化为零,左边关于n的代数式表示为(n+1)2(ax2+bx+c)的形式,化简.然后根据满足条件的等腰三角形有3个,分别判断△>0是否成立.经过计算分别求出K的取值范围即可.
| OA |
| OB |
| OA |
| OB |
(2) ①写出过P的切线,然后分别设出A,B两个点的坐标.根据是已知题意列出3个等式,然后解出结果..通过P点纵坐标为n,代入P中求出n的等量关系.
②按照①的结果,通过把等量关系右边化为零,左边关于n的代数式表示为(n+1)2(ax2+bx+c)的形式,化简.然后根据满足条件的等腰三角形有3个,分别判断△>0是否成立.经过计算分别求出K的取值范围即可.
解答:解:①当k=-2,m=-1,n=-1,
时y=x2+x-2.
切线l:-x-y=2,即x+y+2=0.
由
,
得x2+2x=0,
∴x1=0,x2=-2.
A(0,-2),B(-2,0).
∵
•
=0,|
|=|
|=2.
∴△OAB是等腰直角三角形
②△OAB是以AB为底的等腰三角形?P是AB的中点.
过P点的切线:mx+ny=2.
设A(x1,y1),B(x2,y2),
则
(2)-(1)
y2-y1=(x2+x1)(x2-x1)+x2-x1
=(x2+x1)+1?-
=2m+1,
m=
.
∵m2+n2=2,∴(-
)2+n2=2
4n4+4n3-6n2-8n-2=0
即2n4+2n3-3n2-4n-1=0.
由已知,2n4+2n3-3n2-4n-1
=(n+1)2(an2+bn+c)=(n2+2n+1)(an2+bn+c)
=an4+(b+2a)n3+(c+a+2b)n2+(2c+b)n+c
?
,
即∴
由2n4+2n3-3n2-4n-1=(n+1)2(2n2-2n-1)=0
∴n+1=0或2n2-2n-1=0,
n=-1或n=
∴
或
或
由
得,
nx2+(m+n)x+nk-2=0
当
时,x2+2x+k+2=0.
△=4-4k-8>0,k<-1.
当
时,
x2+x+
k-2=0
由△=1-4×
(
k-2)>0?k<
当
时,
x2+x+
k-2=0,
△=1-4×
(
k-2)>0
(1-
)k>
,
k<
=
k<-
=-1-
.
等腰三角形恰有3个等价于以上三个解都满足△>0,
故k∈(-∞,-1-
).
时y=x2+x-2.
切线l:-x-y=2,即x+y+2=0.
由
|
得x2+2x=0,
∴x1=0,x2=-2.
A(0,-2),B(-2,0).
∵
| OA |
| OB |
| OA |
| OB |
∴△OAB是等腰直角三角形
②△OAB是以AB为底的等腰三角形?P是AB的中点.
过P点的切线:mx+ny=2.
设A(x1,y1),B(x2,y2),
则
|
(2)-(1)
y2-y1=(x2+x1)(x2-x1)+x2-x1
| y2-y1 |
| x2-x1 |
| m |
| n |
m=
| -n |
| 2n+1 |
∵m2+n2=2,∴(-
| n |
| 2n+1 |
4n4+4n3-6n2-8n-2=0
即2n4+2n3-3n2-4n-1=0.
由已知,2n4+2n3-3n2-4n-1
=(n+1)2(an2+bn+c)=(n2+2n+1)(an2+bn+c)
=an4+(b+2a)n3+(c+a+2b)n2+(2c+b)n+c
?
|
即∴
|
由2n4+2n3-3n2-4n-1=(n+1)2(2n2-2n-1)=0
∴n+1=0或2n2-2n-1=0,
n=-1或n=
1±
| ||
| 2 |
∴
|
|
|
由
|
nx2+(m+n)x+nk-2=0
当
|
△=4-4k-8>0,k<-1.
当
|
1+
| ||
| 2 |
1+
| ||
| 2 |
由△=1-4×
1+
| ||
| 2 |
1+
| ||
| 2 |
(
| ||||
| 4 |
当
|
1-
| ||
| 2 |
1-
| ||
| 2 |
△=1-4×
1-
| ||
| 2 |
1-
| ||
| 2 |
(1-
| 3 |
7-
| ||
| 2 |
k<
7-
| ||
2(1-
|
(7-
| ||||
| -4 |
k<-
4+6
| ||
| 4 |
3
| ||
| 2 |
等腰三角形恰有3个等价于以上三个解都满足△>0,
故k∈(-∞,-1-
3
| ||
| 2 |
点评:本题考查直线与圆的关系的应用,通过直线与圆相切,对关系式进行分析.然后通过圆与曲线两个交点再进行分析.通过一系列的运算最终求出结果.本题另外一个侧重点就是对运算的考查与一元二次方程判别式的考查.本题为难题.

练习册系列答案
相关题目
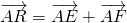 的点R必在圆B上.
的点R必在圆B上.
 的点R必在圆B上.
的点R必在圆B上.