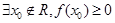题目内容
命题p:函数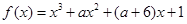 有极大值和极小值;命题 q:抛物线
有极大值和极小值;命题 q:抛物线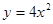 的焦点坐标为(1,0)。若p或q为真命题,p且q为假命题,则实数
的焦点坐标为(1,0)。若p或q为真命题,p且q为假命题,则实数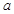 的取值范围是_ _。
的取值范围是_ _。
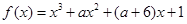 有极大值和极小值;命题 q:抛物线
有极大值和极小值;命题 q:抛物线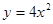 的焦点坐标为(1,0)。若p或q为真命题,p且q为假命题,则实数
的焦点坐标为(1,0)。若p或q为真命题,p且q为假命题,则实数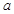 的取值范围是_ _。
的取值范围是_ _。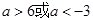
P真: 有两个不同的实数根,所以
有两个不同的实数根,所以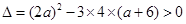 ,解之得
,解之得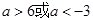 。
。
由于抛物线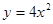 的焦点坐标为
的焦点坐标为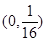 ,所以q为假.
,所以q为假.
由p或q为真命题,p且q为假命题知p真q假。故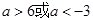 .
.
 有两个不同的实数根,所以
有两个不同的实数根,所以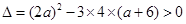 ,解之得
,解之得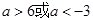 。
。由于抛物线
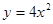 的焦点坐标为
的焦点坐标为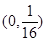 ,所以q为假.
,所以q为假.由p或q为真命题,p且q为假命题知p真q假。故
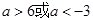 .
.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
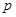 :函数
:函数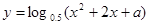 的值域为
的值域为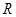 ,命题
,命题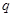 :函数
:函数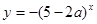 是减函数,若
是减函数,若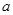 的取值范围是( )
的取值范围是( )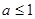
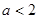
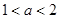
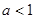 或
或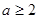
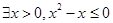 ”的否定是
”的否定是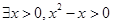
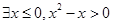
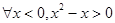
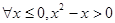
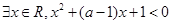 ”是假命题,则实数
”是假命题,则实数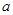 的取值范围是 .
的取值范围是 .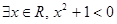 ”的否定是 .
”的否定是 .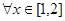 都有x2
都有x2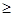 a”。命题q:“
a”。命题q:“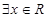 ,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )
,使得x2+2ax+2-a=0成立”,若命题“p且q”是真命题,则实数a的取值范围( )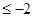
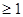
 ,集合
,集合 ,以下命题正确的个数是
,以下命题正确的个数是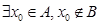 ; ②
; ② ;
; 都有
都有 ; ④
; ④ 都有
都有 .
.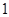


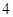
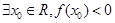 ”的否定是()
”的否定是()