题目内容
13．（2-x2）（1+$\frac{1}{x}$）6的展开式中常数项为（ ）| A． | -28 | B． | -13 | C． | 17 | D． | 32 |
分析 把（1+$\frac{1}{x}$）6按照二项式定理理展开式，可得（2-x2）（1+$\frac{1}{x}$）6的展开式中常数项．
解答 解：（2-x2）（1+$\frac{1}{x}$）6 =（2-x2）（1+${C}_{6}^{1}$•x-1+${C}_{6}^{2}$•x-2+…+${C}_{6}^{6}$•x-6），
故展开式中的常数项为 2-${C}_{6}^{2}$=2-15=-13，
故选：B．
点评 本题主要考查二项式定理的应用，二项展开式的通项公式，属于基础题．
练习册系列答案
相关题目
4．下列事件是随机事件的是（ ）
（1）连续两次掷一枚硬币，两次都出现正面向上．（2）异性电荷相互吸引
（3）在标准大气压下，水在1℃时结冰 （4）任意掷一枚骰子朝上的点数是偶数．
（1）连续两次掷一枚硬币，两次都出现正面向上．（2）异性电荷相互吸引
（3）在标准大气压下，水在1℃时结冰 （4）任意掷一枚骰子朝上的点数是偶数．
| A． | （1）（2） | B． | （2）（3） | C． | （3）（4） | D． | （1）（4） |
1．设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（0＜a＜b）的半焦距为c，（a，0），（0，b）为直线l上两点，已知原点到直线l的距离为$\frac{\sqrt{3}}{4}$c，则双曲线的离心率为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\sqrt{3}$或2 | C． | 2或$\frac{2\sqrt{3}}{3}$ | D． | 2 |
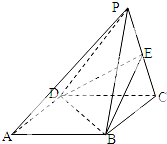如图，四棱锥P-ABCD中，底面ABCD为矩形，PB=PC=AB，PB⊥平面PDC，E为棱PC的中点．