题目内容
命题甲:向量
,
共线,命题乙:向量
,
所在的直线平行.则甲是乙的( )
| a |
| b |
| a |
| b |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
分析:我们可以根据充分、必要条件的定义进行判断.判断充要条件的方法是:
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
①若p?q为真命题且q?p为假命题,则命题p是命题q的充分不必要条件;
②若p?q为假命题且q?p为真命题,则命题p是命题q的必要不充分条件;
③若p?q为真命题且q?p为真命题,则命题p是命题q的充要条件;
④若p?q为假命题且q?p为假命题,则命题p是命题q的即不充分也不必要条件.
解答:解:若向量
,
共线,则向量
,
所在的直线平行或重合,故命题甲不能推出命题乙,甲是乙的不充分条件;
若向量
,
所在的直线平行,则向量
,
共线,正确.即:甲是乙的必要条件;综上所述,甲是乙的必要不充分条件.
故选A.
| a |
| b |
| a |
| b |
若向量
| a |
| b |
| a |
| b |
故选A.
点评:本题考查判断命题p与命题q的关系,关键是掌握充分、必要条件的定义和判断充要条件的方法.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
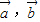 共线,命题乙:向量
共线,命题乙:向量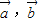 所在的直线平行.则甲是乙的( )
所在的直线平行.则甲是乙的( )