题目内容
已知
，且函数
在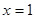
处有极值，则
的最大值等于（ ）
A．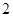
B．3 C．6 D．9
【答案】
D
【解析】
试题分析：求出导函数，利用函数在极值点处的导数值为0得到a，b满足的条件，利用基本不等式求出ab的最大值。解：由题意，求导函数f′（x）=12x2-2ax-2b，∵在x=1处有极值，∴a+b=6，∵a＞0，b＞0，∴ab≤（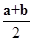
）2=9，当且仅当a=b=3时取等号，所以ab的最大值等于9，故答案为D
考点：基本不等式
点评：本题考查函数在极值点处的导数值为0、考查利用基本不等式求最值，需注意：一正、二定、三相等．
练习册系列答案
相关题目
在
处有极值，设
在
内是单调函数，且当
时，函数
的图象上任一点的切线斜率恒小于
．
的极大值和极小值；
的取值范围．