题目内容
（本题满分12分）一个口袋有2个红球和4个黄球，从中随机地连取3个球，每次取一个，记事件A=“恰有一个红球”，事件B=“第三个是红球”，求：
（1）不放回时，事件A，B的概率；
（2）每次抽后放回时，事件A，B的概率.
（1）不放回时，事件A，B的概率；
（2）每次抽后放回时，事件A，B的概率.
解：（1）基本事件有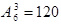
，事件A包含的基本事件有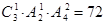
所以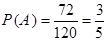
因为第三次抽到红球对前两次没有什么要求，因为红球占总球数的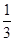
，每次抽到是随机地等可能事件，所以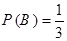
（2）基本事件有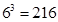
种，事件A包含基本事件有
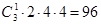种
所以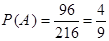
；
第三次抽到红球包括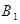
={红，黄，红}，
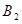={黄，黄，红}，
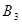={黄，红，红}三种两两互斥，
，
，
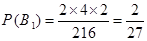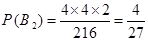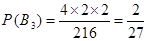
所以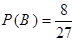
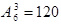，事件A包含的基本事件有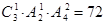所以
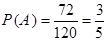
因为第三次抽到红球对前两次没有什么要求，因为红球占总球数的
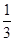，每次抽到是随机地等可能事件，所以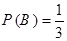（2）基本事件有
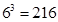种，事件A包含基本事件有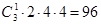种所以
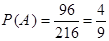；第三次抽到红球包括
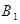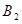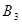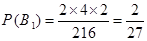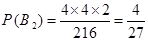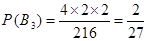
={红，黄，红}，={黄，黄，红}，={黄，红，红}三种两两互斥，，，所以
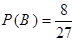
略
练习册系列答案
相关题目
样的零件，第一台出废品的概率是
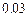，第二台出废品的概率是
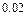．加工出来的零件堆放在一起．若第一台加工的零件是第二台加工的零件的2倍，则任意取出的零件是合格品的概率是 （ ）
，2，3，4，5，6这六个数中一次随机取出两数，则其中一个数是另一个数的两倍的概率等于 ．