题目内容
15.设常数a≥0,函数$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$(1)讨论函数y=f(x)的单调性;
(2)根据a的不同取值,讨论函数y=f(x)的奇偶性,并说明理由.
分析 (1)化简函数,即可得出函数y=f(x)的单调性;
(2)利用分类讨论的思想,若为偶函数求出a的值,若为奇函数,求出a的值,问题得以解决.
解答 解:(1)$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$=1-$\frac{2a}{{2}^{x}+a}$,
∵a≥0,y=$\frac{2a}{{2}^{x}+a}$在R上单调递减,
∴函数y=f(x)在R上单调递增;
(2)若f(x)为偶函数,则f(x)=f(-x)对任意x均成立,
∴$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$=$\frac{{2}^{-x}-a}{{2}^{-x}+a}$,整理可得a(2x-2-x)=0.
∵2x-2-x不恒为0,
∴a=0,此时f(x)=1,x∈R,满足条件;
若f(x)为奇函数,则f(x)=-f(-x)对任意x均成立,
∴$f(x)=\frac{{{2^x}-a}}{{{2^x}+a}}$=-$\frac{{2}^{-x}-a}{{2}^{-x}+a}$,整理可得a2-1=0,
∴a=±1,
∵a≥0,
∴a=1,
此时f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$,x≠0,满足条件;
综上所述,a=0时,f(x)是偶函数,a=1时,f(x)是奇函数.
点评 本题主要考查了函数的单调性、奇偶性,利用了分类讨论的思想,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
6.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{3x-y≤3}\end{array}\right.$,目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )
| A. | [-6,2] | B. | (-6,2) | C. | [-3,1] | D. | (-3,1) |
20.已知i是虚数单位,则$\frac{3-i}{1+i}$的模与虚部的积等于( )
| A. | $2\sqrt{5}i$ | B. | $-2\sqrt{5}i$ | C. | $2\sqrt{5}$ | D. | $-2\sqrt{5}$ |
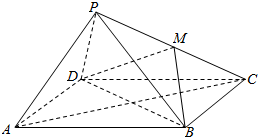 如图已知四边形ABCD是菱形,P是ABCD所在平面外一点,且PB=PD=AB,M是PC的中点,
如图已知四边形ABCD是菱形,P是ABCD所在平面外一点,且PB=PD=AB,M是PC的中点,