题目内容
4.(1)计算:lg25+lg2•lg50(2)设3x=4y=36,求$\frac{2}{x}+\frac{1}{y}$的值.
分析 (1)由已知条件利用对数的性质和运算法则求解.
(2)由已知得x=log336,y=log436,从而$\frac{2}{x}+\frac{1}{y}$=2log363+log364,由此利用对数的运算法则能求出结果.
解答 解:(1)lg25+lg2•lg50
=lg25+lg2(lg5+1)
=lg25+lg2•lg5+lg2
=lg5(lg5+lg2)+lg2
=lg5+lg2
=1.
(2)∵3x=4y=36,
∴x=log336,y=log436,
∴$\frac{2}{x}+\frac{1}{y}$=2log363+log364=log369+log364=1.
点评 本题考查对数的化简求值,是基础题,解题时要认真审题,注意对数的性质和运算法则的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.若f(x)=0在区间(a,b)内恰有一解,则函数f(x)在区间(a,b)内( )
| A. | 单调递减 | B. | 单调递增 | ||
| C. | 单调递减或单调递增 | D. | 不能确定单调性 |
14.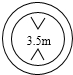 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
 图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )
图中交通标志表示限制高度,即汽车装满货物后,距离地面最大高度不超过3.5米,如果用h表示高度,那么可得如下哪个不等式?( )| A. | h≤3.5 | B. | h≥3.5 | C. | h<3.5 | D. | h>3.5 |