题目内容
设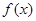 是定义在R上的奇函数,且对任意
是定义在R上的奇函数,且对任意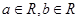 ,当
,当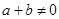 时,都有
时,都有 .
.
(1)求证: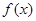 在R上为增函数.
在R上为增函数.
(2)若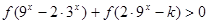 对任意
对任意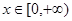 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】
(1) 函数,可知f(-x)=-f(x),则不等式 ,再结合a,b的任意性,和函数单调性定义可得证。
,再结合a,b的任意性,和函数单调性定义可得证。
(2)  . 13分
. 13分
【解析】
试题分析:(1)略 4分
(2)由(1)知 为R上的单调递增函数,
为R上的单调递增函数,
 对任意
对任意 恒成立,
恒成立,
 ,
,
即 ,
7分
,
7分
 ,
, 对任意
对任意 恒成立,
9分
恒成立,
9分
即k小于函数 的最小值.
11分
的最小值.
11分
令 ,则
,则

 . 13分
. 13分
考点:本试题主要是考查了抽象函数的奇偶性和单调性的综合运用,属于中档题。同时结合不等式的知识考查了分析问题和解决问题的能力。
点评:解决该试题的关键是对于已知中函数为奇函数,能将已知的分式不等式翻译为变量差与对应的函数值差,回归到函数的单调性定义上判定和证明,同时利用第一问的结论,去掉抽象函数的符号,转换为求解指数不等式的问题来得到。

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
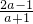 ,则a的取值范围是________.
,则a的取值范围是________. ,则a的取值范围是 .
,则a的取值范围是 .