题目内容
从4名男生和2名女生中任选3人值日,设随机变量ξ表示所选3人中女生的人数.(Ⅰ)求ξ的分布列、数学期望Eξ;
(Ⅱ)求事件“所选3人中女生至少有1人”的概率.
分析:(Ⅰ)依题意可得P(ξ=0)=
,P(ξ=1)=
,P(ξ=2)=
,运算出结果,可得分布列
和数学期望.
(Ⅱ)设“所选3人中女生至少有1人”为事件A,则 P(A)=P(ξ=1)+P(ξ=2).
| ||
|
| ||||
|
| ||||
|
和数学期望.
(Ⅱ)设“所选3人中女生至少有1人”为事件A,则 P(A)=P(ξ=1)+P(ξ=2).
解答:解:(Ⅰ)依题意,得:P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
.
ξ的分布列为: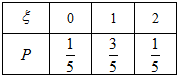
ξ的数学期望:Eξ=0×
+1×
+2×
=1.
(Ⅱ)设“所选3人中女生至少有1人”为事件A,则P(A)=P(ξ=1)+P(ξ=2)=
+
=
.
| ||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 1 |
| 5 |
ξ的分布列为:

ξ的数学期望:Eξ=0×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
(Ⅱ)设“所选3人中女生至少有1人”为事件A,则P(A)=P(ξ=1)+P(ξ=2)=
| 3 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
点评:本题考查求离散型随机变量的分布列,求互斥事件的概率,求出机变量取各个值的概率是解题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
从4名男生和2名女生中任选3人参加演讲比赛,则所选3人中至少有1名女生的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|