题目内容
已知函数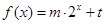 的图像经过点A(0,0),B(3,7)及C
的图像经过点A(0,0),B(3,7)及C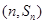 ,
,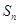 为数列
为数列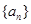 的前n项和
的前n项和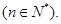
(I)求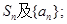
(II)若数列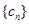 满足
满足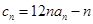 ,求数列
,求数列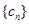 的前n项和
的前n项和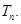
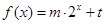 的图像经过点A(0,0),B(3,7)及C
的图像经过点A(0,0),B(3,7)及C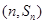 ,
,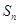 为数列
为数列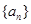 的前n项和
的前n项和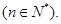
(I)求
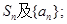
(II)若数列
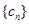 满足
满足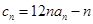 ,求数列
,求数列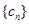 的前n项和
的前n项和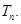
(I)Sn=2n-1(n∈N*an=2n-1(n∈N*).(II)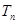 =6(n-1)·2n+1-
=6(n-1)·2n+1- +12
+12
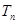 =6(n-1)·2n+1-
=6(n-1)·2n+1- +12
+12本试题主要是考察了数列的通项公式和前n项和的关系式的运用。
(1)因为函数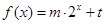 的图像经过点A(0,0),B(3,7)及C
的图像经过点A(0,0),B(3,7)及C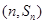 ,则可以得到 f (x)=2x-1,∴Sn=2n-1(n∈N*),从而得到通项公式。
,则可以得到 f (x)=2x-1,∴Sn=2n-1(n∈N*),从而得到通项公式。
(2)由(1)知cn=12nan-n=6n×2n-n.,结合错位相减法得到和式
(I)由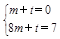 ,得
,得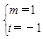 , ……2分
, ……2分
∴f (x)=2x-1,∴Sn=2n-1(n∈N*).……3分
∴当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1. ………4分
当n=1时, S1=a1=1符合上式. ………5分
∴an=2n-1(n∈N*). ………6分
(II)由(1)知cn=12nan-n=6n×2n-n. ………8分
从而Tn=6(1×2+2×22+…+n×2n)-(1+2+…+n)
错位相减法得: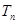 =6(n-1)·2n+1-
=6(n-1)·2n+1- +12.
+12.
(1)因为函数
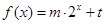 的图像经过点A(0,0),B(3,7)及C
的图像经过点A(0,0),B(3,7)及C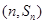 ,则可以得到 f (x)=2x-1,∴Sn=2n-1(n∈N*),从而得到通项公式。
,则可以得到 f (x)=2x-1,∴Sn=2n-1(n∈N*),从而得到通项公式。(2)由(1)知cn=12nan-n=6n×2n-n.,结合错位相减法得到和式
(I)由
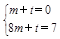 ,得
,得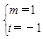 , ……2分
, ……2分∴f (x)=2x-1,∴Sn=2n-1(n∈N*).……3分
∴当n≥2时,an=Sn-Sn-1=2n-2n-1=2n-1. ………4分
当n=1时, S1=a1=1符合上式. ………5分
∴an=2n-1(n∈N*). ………6分
(II)由(1)知cn=12nan-n=6n×2n-n. ………8分
从而Tn=6(1×2+2×22+…+n×2n)-(1+2+…+n)
错位相减法得:
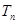 =6(n-1)·2n+1-
=6(n-1)·2n+1- +12.
+12.
练习册系列答案
相关题目
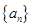 中,
中,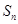 为
为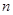 项和,
项和,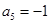 ,
,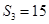 .
.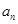 与
与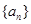 的前
的前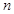 项和为
项和为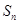 ,点
,点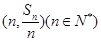 均在函数
均在函数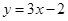 的图像上.
的图像上.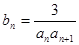 ,
,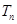 是数列
是数列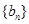 的前
的前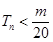 对所有
对所有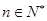 都成立的最小正整数
都成立的最小正整数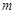 .
.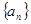 的前
的前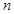 项和为
项和为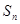 ,且
,且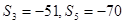 ,
,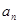 及前
及前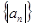 的前14项和
的前14项和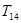 。
。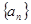 中,
中,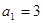 ,其前
,其前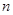 项和为
项和为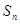 ,等比数列
,等比数列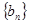 的各项均为正数,
的各项均为正数,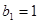 ,公比为
,公比为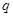 ,且
,且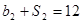 ,
,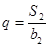 .(Ⅰ)求
.(Ⅰ)求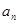 与
与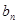 ;(Ⅱ)设数列
;(Ⅱ)设数列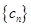 满足
满足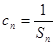 ,求
,求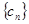 的前
的前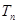 .
.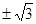
 }的前n项和为Sn,且S3 =6,则5a1+a7,的值为
}的前n项和为Sn,且S3 =6,则5a1+a7,的值为 ,
, ,
, ,则
,则