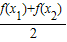题目内容
若f(x)=x2,则对任意实数x1,x2,下列不等式总成立的是( )
A、f(
| ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
分析:欲比较f(
),
的大小,分别考查这两个式子的几何意义,一方面,f(
)是x1,x2中点的函数值;另一方面,
是图中梯形的中位线长,由图即可得出结论.
| x1+x2 |
| 2 |
| f(x1) +f(x2) |
| 2 |
| x1+x2 |
| 2 |
| f(x1) +f(x2) |
| 2 |
解答: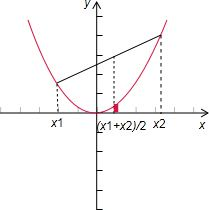 解:如图,在图示的直角梯形中,其中位线的长度为:
解:如图,在图示的直角梯形中,其中位线的长度为:
,
中位线与抛物线的交点到x轴的距离为:f(
),
观察图形可得:f(
)≤
.
故选A.
 解:如图,在图示的直角梯形中,其中位线的长度为:
解:如图,在图示的直角梯形中,其中位线的长度为:| f(x1) +f(x2) |
| 2 |
中位线与抛物线的交点到x轴的距离为:f(
| x1+x2 |
| 2 |
观察图形可得:f(
| x1+x2 |
| 2 |
| f(x1) +f(x2) |
| 2 |
故选A.
点评:本小题主要考查二次函数的性质、二次函数的性质的应用等基础知识,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
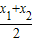 )≤
)≤
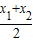 )<
)<
 )≥
)≥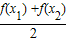
 )>
)>
 )≤
)≤
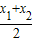 )<
)<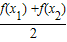
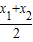 )≥
)≥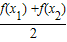
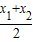 )>
)>