题目内容
已知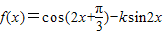 ,且
,且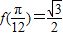 .
.(1)求实数k的值;
(2)求函数f(x)的单调递增区间及最大值,并指出取得最大值时的x值.
【答案】分析:(1)直接利用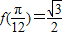 求出实数k的值.
求出实数k的值.
(2)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+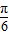 ),由
),由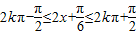 可得x的范围,从而求得函数f(x)的单调递增区间.再根据当
可得x的范围,从而求得函数f(x)的单调递增区间.再根据当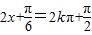 (k∈Z),函数f(x)取得最大值,求出最大值以及最大值时的x值.
(k∈Z),函数f(x)取得最大值,求出最大值以及最大值时的x值.
解答:解:(1)由已知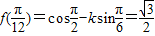 ,得k=-
,得k=-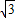 .------(4分)
.------(4分)
(2)∵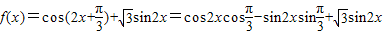
=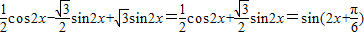 ,--------(8分)
,--------(8分)
由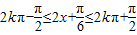 可得
可得 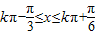 ,
,
∴f(x)的单调递增区间为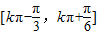 (k∈Z).-------(11分)
(k∈Z).-------(11分)
又当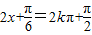 (k∈Z),
(k∈Z),
即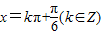 时,函数f(x)取得最大值为1.----------(14分)
时,函数f(x)取得最大值为1.----------(14分)
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,属于中档题.
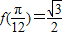 求出实数k的值.
求出实数k的值.(2)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+
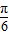 ),由
),由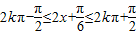 可得x的范围,从而求得函数f(x)的单调递增区间.再根据当
可得x的范围,从而求得函数f(x)的单调递增区间.再根据当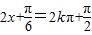 (k∈Z),函数f(x)取得最大值,求出最大值以及最大值时的x值.
(k∈Z),函数f(x)取得最大值,求出最大值以及最大值时的x值.解答:解:(1)由已知
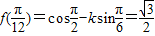 ,得k=-
,得k=-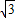 .------(4分)
.------(4分)(2)∵
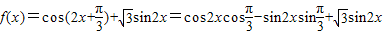
=
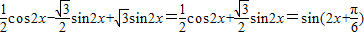 ,--------(8分)
,--------(8分)由
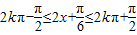 可得
可得 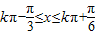 ,
,∴f(x)的单调递增区间为
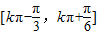 (k∈Z).-------(11分)
(k∈Z).-------(11分)又当
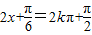 (k∈Z),
(k∈Z),即
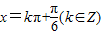 时,函数f(x)取得最大值为1.----------(14分)
时,函数f(x)取得最大值为1.----------(14分)点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和求法,属于中档题.

练习册系列答案
相关题目
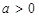 且满足不等式
且满足不等式 。
。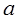 的取值范围。
的取值范围。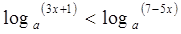 。
。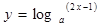 在区间
在区间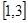 有最小值为
有最小值为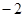 ,求实数
,求实数 值。
值。