题目内容
对于数列{xn},如果存在一个正整数m,使得对任意的n(n∈N*)都有xn+m=xn成立,那么就把这样一类数列{xn}称作周期为m的周期数列,m的最小值称作数列{xn}的最小正周期,以下简称周期.例如当xn=2时,{xn}是周期为1的周期数列,当yn=sin(
n)时,{yn}的周期为4的周期数列.
(1)设数列{an}满足an+2=λ•an+1-an(n∈N*),a1+a,a2=b(a,b不同时为0),且数列{an}是周期为3的周期数列,求常数λ的值;
(2)设数列{an}的前n项和为Sn,且4Sn=(an+1)2.
①若an>0,试判断数列{an}是否为周期数列,并说明理由;
②若anan+1<0,试判断数列{an}是否为周期数列,并说明理由.
(3)设数列{an}满足an+2=-an+1-an(n∈N*),a1=1,a2=2,bn=an+1,数列{bn}的前n项和Sn,试问是否存在p、q,使对任意的n∈N*都有p≤
≤q成立,若存在,求出p、q的取值范围;不存在,说明理由.
| π |
| 2 |
(1)设数列{an}满足an+2=λ•an+1-an(n∈N*),a1+a,a2=b(a,b不同时为0),且数列{an}是周期为3的周期数列,求常数λ的值;
(2)设数列{an}的前n项和为Sn,且4Sn=(an+1)2.
①若an>0,试判断数列{an}是否为周期数列,并说明理由;
②若anan+1<0,试判断数列{an}是否为周期数列,并说明理由.
(3)设数列{an}满足an+2=-an+1-an(n∈N*),a1=1,a2=2,bn=an+1,数列{bn}的前n项和Sn,试问是否存在p、q,使对任意的n∈N*都有p≤
| Sn |
| n |
由(1)数列{an}是周期为3的数列,
得an+3=an,且
?(λ+1)(an+2-an+1)=0,即λ=-1.
(2)当n=1时,s1=a1,4s1=(a1+1)2?a1=1,
当n≥2时,4an=4sn-4sn-1=(an+1)2-(an-1+1)2.?(an-1)2=(an-1+1)2,即an-an-1=2或an=-an-1(n≥2).
①由an>0有an-an-1=2(n≥2),则{an}为等差数列,即an=2n-1,
由于对任意的n都有an+m≠an,所以数列{an}不是周期数列.
②由anan+1<0有an=-an-1(n≥2),数列{an}为等比数列,即an=(-1)n-1,
即an+2=an对任意n都成立.
即当anan+1<0时是{an}周期为2的周期数列.
(3)假设存在p,q.满足题设.
于是
?an+3=an,又bn=an+1则bn+3=bn,
所以{bn}是周期为3的周期数列,所以{bn}的前3项分别为2,3,-2.
则sn=
,
当n=3k时,
=1;
当n=3k-2时,
=1+
?1<
≤2;
当n=3k-1时,
=1+
?1<
≤
,
综上1≤
≤
,
为使p≤
≤q恒成立,只要p≤1,q≥
即可.
综上,存在p≤1,q≥
满足题设.
得an+3=an,且
|
(2)当n=1时,s1=a1,4s1=(a1+1)2?a1=1,
当n≥2时,4an=4sn-4sn-1=(an+1)2-(an-1+1)2.?(an-1)2=(an-1+1)2,即an-an-1=2或an=-an-1(n≥2).
①由an>0有an-an-1=2(n≥2),则{an}为等差数列,即an=2n-1,
由于对任意的n都有an+m≠an,所以数列{an}不是周期数列.
②由anan+1<0有an=-an-1(n≥2),数列{an}为等比数列,即an=(-1)n-1,
即an+2=an对任意n都成立.
即当anan+1<0时是{an}周期为2的周期数列.
(3)假设存在p,q.满足题设.
于是
|
所以{bn}是周期为3的周期数列,所以{bn}的前3项分别为2,3,-2.
则sn=
|
当n=3k时,
| sn |
| n |
当n=3k-2时,
| sn |
| n |
| 1 |
| n |
| sn |
| n |
当n=3k-1时,
| sn |
| n |
| 3 |
| n |
| sn |
| n |
| 5 |
| 2 |
综上1≤
| sn |
| n |
| 5 |
| 2 |
为使p≤
| sn |
| n |
| 5 |
| 2 |
综上,存在p≤1,q≥
| 5 |
| 2 |

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
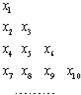 若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足
若一个数列各项取倒数后按原来的顺序构成等差数列,则称这个数列为调和数列.已知数列{an}是调和数列,对于各项都是正数的数列{xn},满足 如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:
如图,设P0是抛物线y=x2上一点,且在第一象限.过点P0作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P0确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论: 如图,设P是抛物线y=x2上一点,且在第一象限.过点P作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论:
如图,设P是抛物线y=x2上一点,且在第一象限.过点P作抛物线的切线,交x轴于Q1点,过Q1点作x轴的垂线,交抛物线于P1点,此时就称P确定了P1.依此类推,可由P1确定P2,….记Pn(xn,yn),n=0,1,2,….给出下列三个结论: