题目内容
22、如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆周上不同于A、B的任一点，求证：平面PAC垂直于平面PBC．
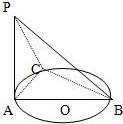
分析：要证明平面PAC垂直于平面PBC，直线证明平面PBC内的直线BC，垂直平面PAC内的两条相交直线PA、AC即可．
解答：证明：连接AC
∵AB是圆O的直径
∴∠ACB=90°即BC⊥AC
又∵PA⊥圆O所在平面，且BC在这个平面内
∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线
∴BC⊥平面PAC∴△PBC所在平面与△PAC所在平面垂直．
∵AB是圆O的直径
∴∠ACB=90°即BC⊥AC
又∵PA⊥圆O所在平面，且BC在这个平面内
∴PA⊥BC 因此BC垂直于平面PAC中两条相交直线
∴BC⊥平面PAC∴△PBC所在平面与△PAC所在平面垂直．
点评：本题考查直线与平面平行与垂直的判定，考查空间想象能力，逻辑思维能力，是基础题．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数