题目内容
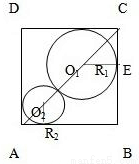
 第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.(1)求这两个内切圆的半径之和;
(2)当这两个圆的半径为何值时,两圆面积之和有最小值?当这两个圆的半径为何值时,两圆面积之和有最大值?
变式(1)在第8题中,若正方形改为矩形,情况又如何?
(2)在第8题中,若正方形改为正方体,圆改为球,情况如何?
分析:(1)由题意可知三角形CEO1为等腰直角三角形,根据勾股定理得到CO1等于
R1;同理得到AO2等于
R2,根据线段AC等于AO2+O2O1+O1C,将各自的值代入即可表示出AC的长,又根据正方形的边长为1,利用勾股定理求出AC的长度,两者相等即可求出两半径之和的值;
(2)根据两圆的半径,利用圆的面积公式表示出两圆的面积之和,由(1)中求出的两半径之和表示出R2,代入两圆的面积之和的式子中消去R2,得到关于R1的关系式,根据完全平方大于等于0求出两圆面积之和的最小值时,两半径的值即可.
变式:(1)设AB=a,AD=b,作直角△O1O2G,利用勾股定理可得(R1+R2)2=[b-(R1+R2)]2+[a-(R1+R2)]2解得R1+R2=(a+b)-
,表示出两圆面积之和S=πR12+πR22,当R1或R2=
min(a,b)时,S有最大值.
(2)球O1和球O2外切,球O1和以C1为顶的三面角的三个面相切,球O2和以A为顶的三面角的三个面相切(设棱长为1),求出两球的体积和,然后利用二次函数求出最大值即可.
| 2 |
| 2 |
(2)根据两圆的半径,利用圆的面积公式表示出两圆的面积之和,由(1)中求出的两半径之和表示出R2,代入两圆的面积之和的式子中消去R2,得到关于R1的关系式,根据完全平方大于等于0求出两圆面积之和的最小值时,两半径的值即可.
变式:(1)设AB=a,AD=b,作直角△O1O2G,利用勾股定理可得(R1+R2)2=[b-(R1+R2)]2+[a-(R1+R2)]2解得R1+R2=(a+b)-
| 2ab |
| 1 |
| 2 |
(2)球O1和球O2外切,球O1和以C1为顶的三面角的三个面相切,球O2和以A为顶的三面角的三个面相切(设棱长为1),求出两球的体积和,然后利用二次函数求出最大值即可.
解答:解:(1)由图知∠CEO1=90°,CE=O1E=R1
∴2R12=CO12,CO1=
R1.
同理AO2=
R2.
∴AC=AO2+O2O1+O1C
=
(R1+R2)+(R1+R2)
=(
+1)(R1+R2),
又∵AB=1,∴AC=
∴(
+1)(R1+R2)=
,
∴R1+R2=
=2-
;
(2)两圆面积之和S=πR12+πR22
=π(R12+R22)=π[R12+(2-
-R1)2]
=π[2R12-2(2-
)R1+(2-
)2]
=2π[(R1-
)2+
].
∴当R1=
,即R1=R2时S为最小.
因R1的最大值为R1=
,这时R2为最小值,其值为R2=(2-
)-
=
-
;
又当R2=
时,R1有最小值R1=
-
,
故当R1=
(此时R2=
-
)或R1=
-
(此时R2=
)时,S有最大值.
变式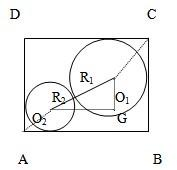 解:(1)如图,ABCD为矩形.
解:(1)如图,ABCD为矩形.
设AB=a,AD=b
作直角△O1O2G则有
(R1+R2)2=[b-(R1+R2)]2+[a-(R1+R2)]2
解之,得R1+R2=(a+b)±
但∵a+b>R1+R2;,
∴R1+R2=(a+b)-
(2)因两圆面积之和S=πR12+πR22
当R1或R2=
min(a,b)时,S有最大值.
如图,球O1和球O2外切,
球O1和以C1为顶的三面角的三个面相切,
球O2和以A为顶的三面角的三个面相切(设棱长为1)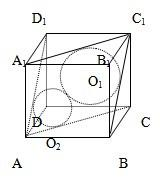
同前类似可计算出AO2=
R2,C1O1=
R1,R1+R2=
.
两球的体积和V=
πR13+
πR23
注:在(1)中的a,b必须限制为b<a≤2b,否则在矩形内之二圆无法相切.
∴2R12=CO12,CO1=
| 2 |
同理AO2=
| 2 |
∴AC=AO2+O2O1+O1C
=
| 2 |
=(
| 2 |
又∵AB=1,∴AC=
| 2 |
∴(
| 2 |
| 2 |
∴R1+R2=
| ||
|
| 2 |
(2)两圆面积之和S=πR12+πR22
=π(R12+R22)=π[R12+(2-
| 2 |
=π[2R12-2(2-
| 2 |
| 2 |
=2π[(R1-
2-
| ||
| 2 |
(2-
| ||
| 4 |
∴当R1=
2-
| ||
| 2 |
因R1的最大值为R1=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
又当R2=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
故当R1=
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
变式
 解:(1)如图,ABCD为矩形.
解:(1)如图,ABCD为矩形.设AB=a,AD=b
作直角△O1O2G则有
(R1+R2)2=[b-(R1+R2)]2+[a-(R1+R2)]2
解之,得R1+R2=(a+b)±
| 2ab |
但∵a+b>R1+R2;,
∴R1+R2=(a+b)-
| 2ab |
(2)因两圆面积之和S=πR12+πR22
|
当R1或R2=
| 1 |
| 2 |
如图,球O1和球O2外切,
球O1和以C1为顶的三面角的三个面相切,
球O2和以A为顶的三面角的三个面相切(设棱长为1)

同前类似可计算出AO2=
| 3 |
| 3 |
3-
| ||
| 2 |
两球的体积和V=
| 4 |
| 3 |
| 4 |
| 3 |
|
|
|
|
|
|
|
注:在(1)中的a,b必须限制为b<a≤2b,否则在矩形内之二圆无法相切.
点评:此题考查学生掌握正方形的性质,掌握直线与圆相切时所满足的条件以及两圆外切时所满足的条件,是一道多知识的综合题.变式题主要考查了长方形的两个内切圆,以及正方体的内切球和球的性质,同时考查了空间想象能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目