题目内容
已知等差数列{an}的前n项和为 Sn
(I)若a1=1,S10= 100,求{an}的通项公式;
(II)若Sn=n2-6n,解关于n的不等式Sn+an>2n
(I)若a1=1,S10= 100,求{an}的通项公式;
(II)若Sn=n2-6n,解关于n的不等式Sn+an>2n
(I)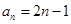 ; (II)
; (II)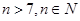 .
.
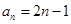 ; (II)
; (II)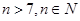 .
.试题分析:(I)要求等差数列的通项公式,由已知条件只需再找到d即可,由
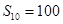 结合等差数列的前n项和公式很快即可解决该问题; (II)先由
结合等差数列的前n项和公式很快即可解决该问题; (II)先由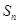 ,结合
,结合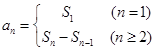 求出该等差数列的通项
求出该等差数列的通项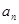 ,代入条件即可将该问题转化为一元二次不等式的问题.
,代入条件即可将该问题转化为一元二次不等式的问题.试题解析:
(I)设
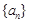 的公差为
的公差为
因为
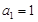 ,
,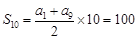 2分
2分所以
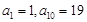 4分
4分所以
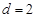
所以
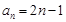 ; 6分
; 6分(II)因为
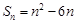
当
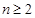 时,
时,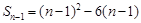
所以
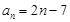 ,
,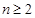 9分
9分又
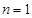 时,
时,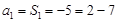
所以
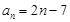 10分
10分所以
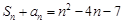
所以
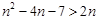 ,即
,即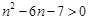
所以
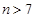 或
或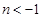 ,
,所以
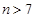 ,
,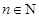 . 13分
. 13分
练习册系列答案
相关题目
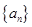 的首项
的首项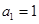 ,前
,前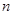 项和
项和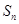 满足
满足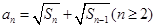 .
.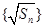 为等差数列,并求数列
为等差数列,并求数列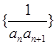 的前
的前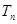 ,若对任意的
,若对任意的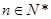 ,不等式
,不等式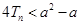 恒成立,求实数
恒成立,求实数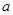 的取值范围.
的取值范围.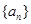 中,
中,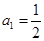 ,点
,点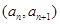 在直线
在直线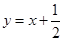 上.
上.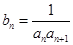 ,求数列
,求数列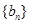 的前n项和
的前n项和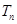 .
.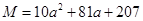 ,
,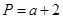 ,Q=
,Q= ;若将
;若将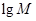 ,lgQ,lgP适当排序后可构成公差为1的等差数列
,lgQ,lgP适当排序后可构成公差为1的等差数列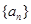 的前三项.
的前三项.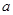 的值及
的值及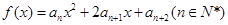 的图象在
的图象在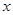 轴上截得的线段长为
轴上截得的线段长为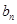 ,
,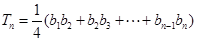
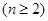 ,求
,求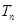 ,并证明
,并证明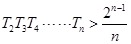 .
.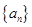 ,
,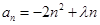 ,若该数列是递减数列,则实数
,若该数列是递减数列,则实数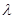 的取值范围是( )
的取值范围是( )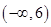
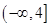
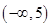
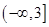
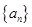 的前
的前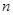 项和为
项和为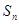 ,
,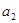 、
、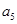 是方程
是方程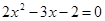 的两个根,
的两个根,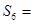 ( )
( )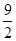
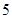
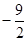
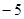
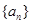 是公比大于
是公比大于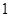 的等比数列,
的等比数列,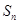 是
是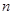 项和.若
项和.若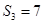 ,且
,且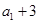 ,
,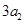 ,
,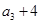 构成等差数列.
构成等差数列.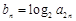 ,求数列
,求数列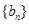 的前
的前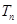 .
.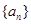 的前n项和为
的前n项和为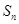 .已知
.已知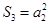 ,且
,且 成等比数列,求
成等比数列,求