题目内容
18.如果f(x)=$\left\{\begin{array}{l}{-2,}&{x>0}\\{0,}&{x=0}\\{2,}&{x<o}\end{array}\right.$ 那么f[f(-5)]=-2.分析 根据题意,由函数的解析式,分析可得f(-5)=2,进而由2>0分析可得f(2)=-2,综合可得f[f(-5)]=f(2)=-2,即可得答案.
解答 解:根据题意,f(x)=$\left\{\begin{array}{l}{-2,}&{x>0}\\{0,}&{x=0}\\{2,}&{x<o}\end{array}\right.$,
对于x=-5,由于-5<0,则f(-5)=2,
当x=2时,2>0,则有f(2)=-2,
则f[f(-5)]=f(2)=-2,
故答案为:-2.
点评 本题函数值的计算,涉及分段函数的运用,注意认真分析分段函数的解析式.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
6.若三点A(0,a,2b),B(2,3,4),C(3,4,5)共线,则下列等式成立的是( )
| A. | 2a=b | B. | a+b=2 | C. | 2a-b=3 | D. | a-2b=1 |
3.若非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,且|$\overrightarrow{a}$-$\overrightarrow{b}$|=2|$\overrightarrow{a}$|,则向量$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
10.已知sin(π-α)=-$\frac{2}{5}$,且α是第四象限角,则tanα=( )
| A. | $\frac{2\sqrt{21}}{21}$ | B. | -$\frac{2\sqrt{21}}{21}$ | C. | -$\frac{2}{3}$ | D. | $\frac{\sqrt{21}}{2}$ |
8.函数f(x)=x2-4x-lnx+4的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
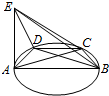 已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).
已知三棱锥E-ABD各个面均为直角三角形,且Rt△ADE的直角顶点为A,其中AE=AB,∠ABD=$\frac{π}{6}$,以AB为直径在平面ABD内画圆,且经过点D,任取圆上一点C(不与A,B两点重合).