题目内容
15.函数$f(x)=\frac{{\sqrt{3x-{x^2}}}}{x-2}$的定义域为[0,2)∪(2,3].分析 由根式内部的代数式大于等于0,分式的分母不为0联立不等式组得答案.
解答 解:由$\left\{\begin{array}{l}{3x-{x}^{2}≥0}\\{x-2≠0}\end{array}\right.$,解得0≤x≤3,且x≠2.
∴函数$f(x)=\frac{{\sqrt{3x-{x^2}}}}{x-2}$的定义域为[0,2)∪(2,3].
故答案为:[0,2)∪(2,3].
点评 本题考查函数的定义域及其求法,考查一元二次不等式的解法,是基础题.

练习册系列答案
相关题目
6.在复平面内,复数z=$\frac{1}{1+i}+{i^3}$所对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.集合A={1,2}的非空真子集个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.记x=log34•log56•log78,y=log45•log67•log89,则( )
| A. | x$<y<\sqrt{2}$ | B. | $\sqrt{2}$<x<y | C. | y$<\sqrt{2}$<x | D. | $\sqrt{2}$<y<x |
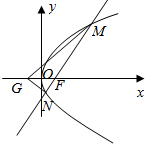 已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2
已知点F是抛物线C:y2=2px(p>0)的焦点,点A(m,2)在抛物线C上,且AF=2