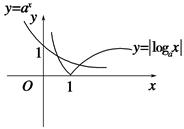
题目内容
已知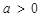 ,函数
,函数 在区间
在区间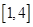 上的最大值等于
上的最大值等于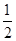 ,则
,则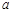 的值为 .
的值为 .
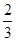 或
或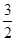
解析试题分析:有已知得 ,因为
,因为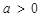 ,所以
,所以 在
在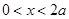 时递减,在
时递减,在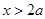 是递增,因此在
是递增,因此在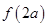 处有最小值,即在区间端点处取最大值,若
处有最小值,即在区间端点处取最大值,若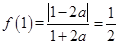 ,得
,得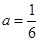 或
或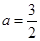 ,检验若
,检验若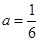 则
则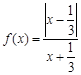 在
在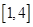 上单调递增,
上单调递增,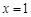 处不能取最大值,所以不符合.若
处不能取最大值,所以不符合.若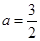 则
则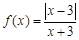 在
在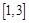 单调递减,在
单调递减,在 单调递增,此时
单调递增,此时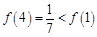 ,所以
,所以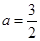 满足题意;同理若
满足题意;同理若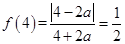 得
得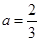 或
或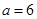 ,同理经检验
,同理经检验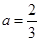 符合,
符合,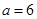 不符合.
不符合.
考点: 1.含绝对值不等式,去绝对值;2.函数单调性及最值;

练习册系列答案
 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
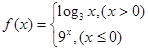 ,则
,则 .
.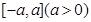 内图像不间断的函数
内图像不间断的函数 满足
满足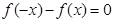 ,函数
,函数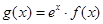 ,且
,且 ,又当
,又当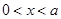 时,有
时,有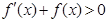 ,则函数
,则函数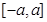 内零点的个数是________。
内零点的个数是________。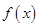 的图像经过(0,1)点,则函数
的图像经过(0,1)点,则函数 的反函数的图像必经过点 .
的反函数的图像必经过点 .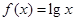 ,若
,若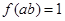 ,则
,则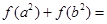 _________.
_________.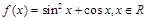 的最大值等于 .
的最大值等于 .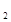 (x
(x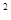 -2x+3)有以下4个结论:其中正确的有 .
-2x+3)有以下4个结论:其中正确的有 .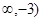
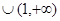 ; ② 递增区间为
; ② 递增区间为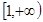 ;
;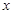 轴的上方.
轴的上方. 的值域为 .
的值域为 .