题目内容
以原点为圆心，且与直线x+y-2=0相切的圆的方程为
- A.
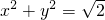
- B.x2+y2=2
- C.x2+y2=4
- D.x2-y2=2
B
分析：求出原点到直线的距离，就是所求圆的半径，然后弦长所求圆的方程．
解答：原点到直线的距离为：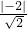
=
．它就是所求圆的半径，
所以以原点为圆心，且与直线x+y-2=0相切的圆的方程为x2+y2=2．
故选B．
点评：本题是基础题，考查圆的方程的求法，考查计算能力．
分析：求出原点到直线的距离，就是所求圆的半径，然后弦长所求圆的方程．
解答：原点到直线的距离为：
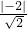=．它就是所求圆的半径，所以以原点为圆心，且与直线x+y-2=0相切的圆的方程为x2+y2=2．
故选B．
点评：本题是基础题，考查圆的方程的求法，考查计算能力．
练习册系列答案
相关题目
的离心率为
，直线
:
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切.
，右焦点
，直线
过点
垂
，线段
垂直平分线交
，求点
的方程；
轴上时，在曲线
的离心率为
，
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切。
过点F1，且垂直于椭圆的长轴，动直
垂直
的离心率为
，
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切。
过点F1，且垂直于椭圆的长轴，动直
垂直