题目内容
 已知函数y=2cos(
已知函数y=2cos(| 1 |
| 2 |
| π |
| 4 |
(1)用“五点法”作出这个函数在一个周期内的图象;
(2)函数y=cosx图象经过怎样的变换可以得到y=2cos(
| 1 |
| 2 |
| π |
| 4 |
分析:(1)用五点法作函数y=Asin(ωx+∅)在一个周期上的简图.
(2)根据函数y=Asin(ωx+∅)的图象的变换规律,得出结论.
(2)根据函数y=Asin(ωx+∅)的图象的变换规律,得出结论.
解答:解:(1)列表:
作图: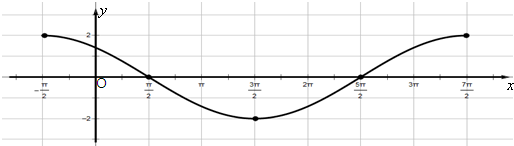
(2)把y=cosx的图象向左平移
个单位得到y=cos(x+
)的图象,再把y=cos(x+
)的图象纵坐标不变,
横坐标变为原来的2倍得到y=cos(
x+
)的图象,
最后把y=cos(
x+
)的图象横坐标不变,纵坐标变为原来的2倍,得到y=2cos(
x+
)的图象. …(10分)
| x | -
|
|
|
|
| ||||||||||
|
0 |
|
π |
|
2π | ||||||||||
y=2cos(
|
2 | 0 | -2 | 0 | 2 |

(2)把y=cosx的图象向左平移
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
横坐标变为原来的2倍得到y=cos(
| 1 |
| 2 |
| π |
| 4 |
最后把y=cos(
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
点评:本题主要考查用五点法作函数y=Asin(ωx+∅)在一个周期上的简图,函数y=Asin(ωx+∅)的图象的变换规律,属于中档题.

练习册系列答案
相关题目

