题目内容
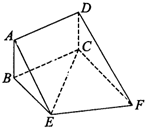 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=| 3 |
EF=2.
(1)求异面直线AD与EF所成的角;
(2)当二面角D-EF-C的大小为45°时,求二面角A-EC-B的正切值.
分析:如图,以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系 C-xyz,设出AB,BE,CF,求出C,A,B,E,F,D的坐标,(1)求出cos<
,
>=
中的有关向量,即可求出所求角的大小.
(2)求出平面AEC的法向量
,通过cos<
,
>=
,即可求解二面角A-EC-B的正切值.
| DA |
| FE |
| ||||
|
|
(2)求出平面AEC的法向量
| n |
| n |
| BA |
| ||||
|
|
解答:解:如图,以点C为坐标原点,以CB,CF和CD分别为作x轴,y轴和z轴,建立空间直角坐标系 C-xyz.…(1分)
F(0,c,0),D(0,0,a)…(2分)
(1)
=(
,0,0),
=(
,0,0),
=(
,b-c,0),
由|
|=2,得3+(b-c)2=4,∴b-c=-1.…(4分)
所以
=(
,-1,0).
所以cos<
,
>=
=
=
,…(5分)
所以异面直线AD与EF成30° …(6分)
(2)当二面角D-EF-C的大小为45,即∠DEC=45°.
设
=(1,y,z)为平面AEC的法向量,则
•
=0,
•
=0,
求得
=(1,-
,-
).…(8分)
又因为BA⊥平面BEFC,
=(0,0,1),
所以cos<
,
>=
=-
…(10分)
sin<
,
>=
═
=
,
tan<
,
>=
=
.
∴二面角A-EC-B的正切值为
,.…(12分)
|
F(0,c,0),D(0,0,a)…(2分)
(1)
| DA |
| 3 |
| CB |
| 3 |
| FE |
| 3 |
由|
| FE |
所以
| FE |
| 3 |
所以cos<
| DA |
| FE |
| ||||
|
|
| 3 | ||
|
| ||
| 2 |
所以异面直线AD与EF成30° …(6分)
(2)当二面角D-EF-C的大小为45,即∠DEC=45°.

设
| n |
| n |
| AE |
| n |
| EC |
求得
| n |
| ||
| 3 |
| 1 |
| 2 |
又因为BA⊥平面BEFC,
| BA |
所以cos<
| n |
| BA |
| ||||
|
|
| ||
| 19 |
sin<
| n |
| BA |
1-cos2<
|
1-(-
|
4
| ||
| 19 |
tan<
| n |
| BA |
| ||||
-
|
4
| ||
| 3 |
∴二面角A-EC-B的正切值为
4
| ||
| 3 |
点评:本题是中档题,考查异面直线所成的角,二面角的求法,考查空间想象能力,计算能力.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
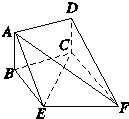 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD= 如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=
如图,矩形ABCD和梯形BEFC所在的平面互相垂直,BE∥CF,BE<CF,∠BCF=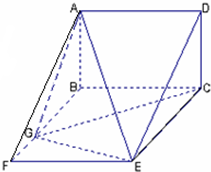 如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,
如图,矩形ABCD和矩形BCEF所在平面互相垂直,G为边BF上一点,∠CGE=90°,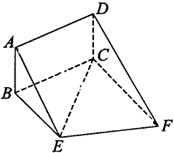 如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=
如图,矩形ABCD和直角梯形BEFC所在平面互相垂直,∠BCF=90°,BE∥CF,CE⊥EF,AD=