题目内容
(I)给定数列{cn},如果存在实常数p,q,使得cn+1=pcn+q对于任意n∈N*都成立,则称数列{cn}是“M类数列”.
(i)若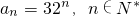 ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
(ii)若数列{bn}的前n项和为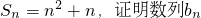 是“M类数列”.
是“M类数列”.
(Ⅱ)若数列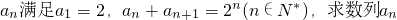 前2013项的和.
前2013项的和.
解:(Ⅰ)(i)∵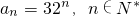 ,
,
∴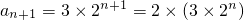 =2×an=2an+0,
=2×an=2an+0,
∴p=2,q=0
∴数列{an}是“M”数列.
(ii)当n=1时,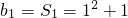 =2.
=2.
当n≥2时,bn=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
上式对于n=1时也成立,
∴bn=2n(n∈N*).
∴bn+1=2(n+1)=2n+2=bn+2.
∴数列{bn}是“M”数列,且p=1,q=2.
(Ⅱ)∵ (n∈N*),∴
(n∈N*),∴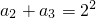 ,
,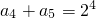 ,…
,…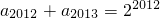 .
.
S2013=a1+a2+a3+…+a2013=2+22+24+…+22012= =
= .
.
故数列{an}前2013项的和S2013= .
.
分析:(Ⅰ)(i)由an的表达式即可得出an+1的表达式,再利用“M”数列的定义进行判断即可.
(ii)利用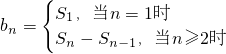 先求出数列{bn}的通项公式,再利用“M”数列的定义进行判断即可.
先求出数列{bn}的通项公式,再利用“M”数列的定义进行判断即可.
(Ⅱ)根据数列{an}满足的条件:a1=2, ,分别令n=2,4,…2012.将以上这些式子相加即可得出S2013.
,分别令n=2,4,…2012.将以上这些式子相加即可得出S2013.
点评:理解“M”数列的定义及充分利用已知条件和数列求和的公式与方法是解题的关键.
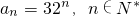 ,
,∴
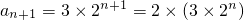 =2×an=2an+0,
=2×an=2an+0,∴p=2,q=0
∴数列{an}是“M”数列.
(ii)当n=1时,
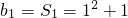 =2.
=2.当n≥2时,bn=Sn-Sn-1=n2+n-(n-1)2-(n-1)=2n.
上式对于n=1时也成立,
∴bn=2n(n∈N*).
∴bn+1=2(n+1)=2n+2=bn+2.
∴数列{bn}是“M”数列,且p=1,q=2.
(Ⅱ)∵
 (n∈N*),∴
(n∈N*),∴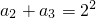 ,
,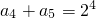 ,…
,…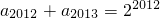 .
.S2013=a1+a2+a3+…+a2013=2+22+24+…+22012=
 =
= .
.故数列{an}前2013项的和S2013=
 .
.分析:(Ⅰ)(i)由an的表达式即可得出an+1的表达式,再利用“M”数列的定义进行判断即可.
(ii)利用
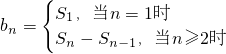 先求出数列{bn}的通项公式,再利用“M”数列的定义进行判断即可.
先求出数列{bn}的通项公式,再利用“M”数列的定义进行判断即可.(Ⅱ)根据数列{an}满足的条件:a1=2,
 ,分别令n=2,4,…2012.将以上这些式子相加即可得出S2013.
,分别令n=2,4,…2012.将以上这些式子相加即可得出S2013.点评:理解“M”数列的定义及充分利用已知条件和数列求和的公式与方法是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;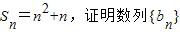 是“M类数列”.
是“M类数列”. 前2013项的和.
前2013项的和.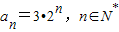 ,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由;
,数列{an}是否为“M类数列”?若是,指出它对应的实常数p,q,若不是,请说明理由; 是“M类数列”.
是“M类数列”.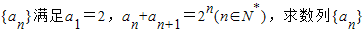 前2013项的和.
前2013项的和.