题目内容
(本小题满分12分)
设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn="2" an-3n .
(1)求证{ an+3}是等比数列
 (2)求数列{an}的通项公式;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和Sn .
设数列{an}的前n项和为Sn,若对于任意的n∈N*,都有Sn="2" an-3n .
(1)求证{ an+3}是等比数列
 (2)求数列{an}的通项公式;
(2)求数列{an}的通项公式;(3)求数列{an}的前n项和Sn .
解:(1)令n=1,S1=2a1-3. ∴a1 ="3 " 又Sn+1=2an+1-3(n+1), Sn=2an-3n,两式相减得,
an+1 =2an+1-2an-3,则an+1 =2an+3 (2){ an+3}是公比为2的等比数列.则
an+3=(a1+3)·2n-1=6·2n-1, ∴an =6·2n-1-3 . (3)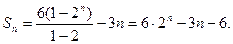
an+1 =2an+1-2an-3,则an+1 =2an+3 (2){ an+3}是公比为2的等比数列.则
an+3=(a1+3)·2n-1=6·2n-1, ∴an =6·2n-1-3 . (3)
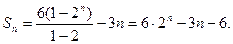
略

练习册系列答案
相关题目
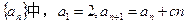 (c是常数,
(c是常数,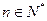 )且
)且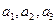 成公比不为1的等比数列。
成公比不为1的等比数列。
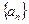 的通项公式。
的通项公式。 中,
中, ,且
,且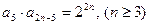 ,则当
,则当
 时,
时, ( )
( )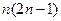



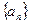 中,
中,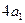
 ,
,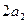 ,
,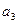 成等差数列,若
成等差数列,若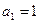 ,则
,则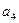 =" " ( )
=" " ( )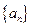 的前
的前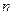 项和为
项和为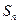 ,点
,点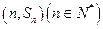 在函数
在函数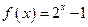 的图象上,则数列
的图象上,则数列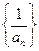 的前
的前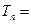 _______________
_______________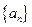 中,
中,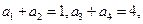 则
则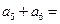 ___.
___.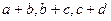 也成等比数列;
也成等比数列;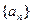 既是等差数列,也是等比数列,则
既是等差数列,也是等比数列,则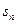 ,且
,且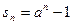 ,(a
,(a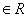 ),则
),则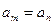
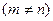
 中,
中, ,且
,且 ,则
,则 等于( )
等于( )