题目内容
（本题满分12分）
甲、乙、丙三人进行象棋比赛，每两人比赛一场，共赛三场．每场比赛胜者得3
分，负者得0分，没有平局，在每一场比赛中，甲胜乙的概率为
，甲胜丙的概率为
，乙胜丙的概率为
(1)求甲获第一名且丙获第二名的概率：
(2)设在该次比赛中，甲得分为ξ，求ξ的分布列和数学期望。
【答案】
解：(1)甲获第一，则甲胜乙且甲胜丙，
∴甲获第一的概率为
……………2分
丙获第二，则丙胜乙，其概率为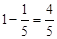
…………4分
∴甲获第一名且丙获第二名的概率为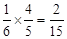
……………6分
(2)ξ可能取的值为O、3、6…………………………7分
甲两场比赛皆输的概率为
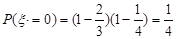……8分
甲两场只胜一场的概率为
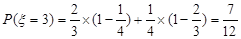………9分
甲两场皆胜的概率为
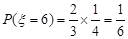……………lO分
∴ξ的分布列为
ξ 0 3 6
P 
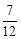
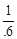
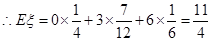…………l2分
【解析】略
练习册系列答案
相关题目
是首项为
，公比
的等比数列，，
，数列
.
的通项公式；（2）求数列
的前n项和Sn.
<1，xÎR }．
，求实数a的取值范围．
（
，
为常数），且方程
有两个实根为
.
的解析式；
中，四边形
是边长为
的正方形，
，
为
上的点，且
⊥平面
⊥平面
的大小；
到平面