题目内容
(本题13分)设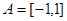 ,
,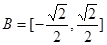 ,函数
,函数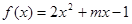 ,
,
(1)设不等式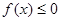 的解集为C,当
的解集为C,当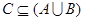 时,求实数
时,求实数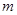 取值范围;
取值范围;
(2)若对任意 ,都有
,都有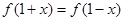 成立,求
成立,求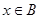 时,
时,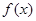 的值域;
的值域;
(3)设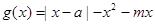
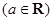 ,求
,求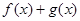 的最小值.
的最小值.
【答案】
(1)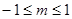 (2)
(2)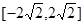 (3)
(3)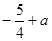
【解析】本试题主要是研究二次函数的 性质的运用。利用函数的单调性和不等式的知识的综合运用得到。
(1)根据不等式的解集得到C,然后利用集合的并集和集合间的关系得到实数m的范围
(2)根据对于任意的实数都有函数式子成立,说明函数的对称轴x=1,然后得到解析式,从而求解给定区间的值域。
(3)利用给定的函数,结合二次函数的图像与性质得到最值。
解:(1)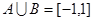 ,因为
,因为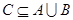 ,
,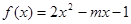 图像开口向上,
图像开口向上,
且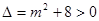 恒成立,故图像始终与
恒成立,故图像始终与 轴有两个交点,由题意,要使这两个交点横坐标
轴有两个交点,由题意,要使这两个交点横坐标
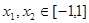 ,当且仅当:
,当且仅当: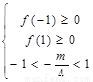 ,………3分,解得:
,………3分,解得: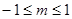 ……4分
……4分
(2)对任意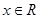 都有
都有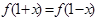 ,所以
,所以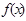 图像关于直线
图像关于直线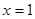 对称,所以
对称,所以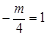 ,
,
得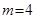 .所以
.所以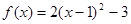 为
为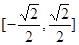 上减函数.
上减函数.
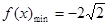 ;
;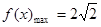 .故
.故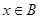 时,
时,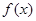 值域为
值域为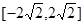 6分(3)令
6分(3)令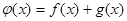 ,则
,则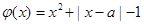
(i)当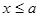 时,
时,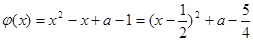 ,当
,当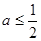 ,
,
则函数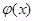 在
在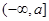 上单调递减,从而函数
上单调递减,从而函数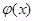 在
在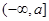 上的最小值为
上的最小值为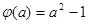 .
.
若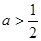 ,则函数
,则函数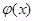 在
在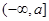 上的最小值为
上的最小值为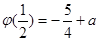 ,且
,且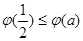
(ii)当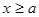 时,函数
时,函数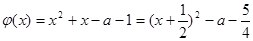 ,若
,若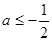 ,
,
则函数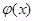 在
在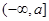 上的最小值为
上的最小值为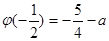 ,且
,且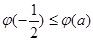 ,若
,若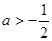 ,
,
则函数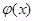 在
在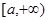 上单调递增,
上单调递增,
从而函数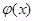 在
在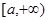 上的最小值为
上的最小值为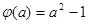 .…………………………1分
.…………………………1分
综上,当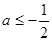 时,函数
时,函数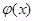 的最小值为
的最小值为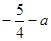 ,当
,当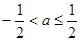 时,
时,
函数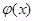 的最小值为
的最小值为
当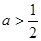 时,函数
时,函数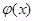 的最小值为
的最小值为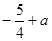 . 13分GH
. 13分GH

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 的左右焦点分别为
的左右焦点分别为 ,
, ,上顶点为
,上顶点为 ,过点
,过点 垂直的直线交
垂直的直线交 轴负半轴于
轴负半轴于 点,且
点,且 是
是 的中点.
的中点.
 的圆恰好与直线
的圆恰好与直线 相切,求椭圆
相切,求椭圆 的方程;
的方程; 作斜率为
作斜率为 的直线
的直线 与椭圆相交于
与椭圆相交于 两点,在
两点,在 使得以
使得以 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。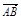 =a+b,
=a+b,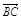 =2a+8b,
=2a+8b,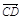 =3(a-b),求证:A、B、D三点共线;
=3(a-b),求证:A、B、D三点共线;