题目内容

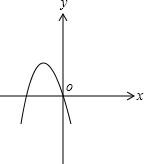
精英家教网定义在R上的函数y=f（x）的图象经过坐标原点O，且它的导函数y=f′（x）的图象是如图所示的一条直线，则y=f（x）的图象一定不经过第
 
象限．
分析：根据导函数的图象和函数f（x）过原点，设出f（x）的解析式f（x）=ax2+bx，得到函数f（x）为开口向下的抛物线，求出导函数f'（x）=2ax+b，根据一次函数的图象的特点得到a与b的正负，即可判断出二次函数顶点所在的象限，开口向下，结合f（0）=0，可知图象不过第一象限．
解答：解：由导函数的图象可知f（x）=ax2+bx，故f'（x）=2ax+b，∴a＜0，b＜0．
函数f（x）=ax2+bx图象的顶点（-
b
2a
，
-b2
4a
）在第二象限，且f（0）=0，可知图象不过第一象限．
精英家教网
故答案为：一
点评：本题考查了函数的单调性与导数之间的关系，考查了数学转化思想方法，考查了二次函数图象的顶点坐标，是基础题．
练习册系列答案
相关题目
11、定义在R上的函数y=f（x）满足f（-x）=-f（x），f（1+x）=f（1-x），当x∈[-1，1]时，f（x）=x3，则f（2009）的值是（　　）
13、定义在R上的函数y=f（x）满足：f（x）=f（4-x），且f（x-2）+f（2-x）=0，则f（508）=
0
．
定义在R上的函数y=f(x)满足f(3-x)=f(x)，(x-
3
2
)f′(x)＞0(x≠
3
2
)，若x1＜x2，且x1+x2＞3，则有（　　）
下列四个命题：
①“a＞b”是“2a＞2b”成立的充要条件；
②“a=b”是“lga=lgb”成立的充分不必要条件；
③函数f（x）=ax2+bx（x∈R）为奇函数的充要条件是“a=0”
④定义在R上的函数y=f（x）是偶函数的必要条件是“
f(-x)f(x)
=1”．
其中真命题的序号是
①③
①③
．（把真命题的序号都填上）
定义在R上的函数y=f（x）满足f（-x）=-f（x），f（1+x）=f（1-x），当x∈[-1，1]时，f（x）=x3，则f（2011）=
-1
-1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网