题目内容
以原点为圆心的圆全部在区域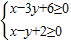 内,则圆的面积的最大值为( )
内,则圆的面积的最大值为( )A.
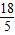 π
πB.
 π
πC.2π
D.π
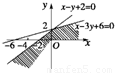
【答案】分析:已知原点为圆心的圆全部在区域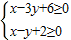 内,画出可行域,发现只有圆与直线x-y+2=0相切时,圆的半径最大,从而求解.
内,画出可行域,发现只有圆与直线x-y+2=0相切时,圆的半径最大,从而求解.
解答:解:据条件画出线性可行域,结合图形,要使得以原点为圆心的圆的半径最大,
根据点到直线的距离公式可知,原点到直线x-y+2=0的距离为:d1=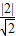 =
=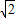 ,
,
∵以原点为圆心的圆的半径大于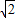 时,由所画图中的阴影部分的可行域可知此时圆有部分面积不在此可行域内,
时,由所画图中的阴影部分的可行域可知此时圆有部分面积不在此可行域内,
∴只有圆与直线x-y+2=0相切时,圆的半径最大R=d1,
即R=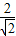 =
=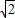 ,
,
此时圆的最大面积为S=π(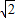 )2=2π.
)2=2π.
故选C.
点评:此题主要考查简单线性规划的应用,此类题高考一般考一道选择题,比较简单.
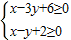 内,画出可行域,发现只有圆与直线x-y+2=0相切时,圆的半径最大,从而求解.
内,画出可行域,发现只有圆与直线x-y+2=0相切时,圆的半径最大,从而求解.解答:解:据条件画出线性可行域,结合图形,要使得以原点为圆心的圆的半径最大,
根据点到直线的距离公式可知,原点到直线x-y+2=0的距离为:d1=
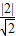 =
=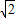 ,
,∵以原点为圆心的圆的半径大于
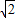 时,由所画图中的阴影部分的可行域可知此时圆有部分面积不在此可行域内,
时,由所画图中的阴影部分的可行域可知此时圆有部分面积不在此可行域内,∴只有圆与直线x-y+2=0相切时,圆的半径最大R=d1,
即R=
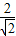 =
=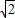 ,
,
此时圆的最大面积为S=π(
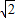 )2=2π.
)2=2π.故选C.
点评:此题主要考查简单线性规划的应用,此类题高考一般考一道选择题,比较简单.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
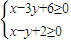 内,则圆的面积的最大值为( )
内,则圆的面积的最大值为( )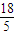 π
π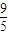 π
π