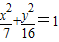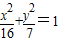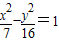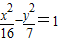题目内容
已知动圆P过定点A（-3，0），并且与定圆B：（x-3）2+y2=64内切，则动圆的圆心P的轨迹是（ ）
分析：设动圆P和定圆B内切于M，则动圆的圆心P到两点，即定点A（-3，0）和定圆的圆心B（3，0）的距离之和恰好等于定圆半径，根据椭圆的定义，可得结论．
解答：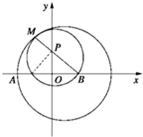
解：如图，设动圆P和定圆B内切于M，则动圆的圆心P到两点，即定点A（-3，0）和定圆的圆心B（3，0）的距离之和恰好等于定圆半径，
即|PA|+|PB|=|PM|+|PB|=|BM|=8．
∴点P的轨迹是以A、B为焦点的椭圆，
故选D．
解：如图，设动圆P和定圆B内切于M，则动圆的圆心P到两点，即定点A（-3，0）和定圆的圆心B（3，0）的距离之和恰好等于定圆半径，即|PA|+|PB|=|PM|+|PB|=|BM|=8．
∴点P的轨迹是以A、B为焦点的椭圆，
故选D．
点评：本题重点考查轨迹方程的探求，解题的关键是利用两圆的位置关系，得出动圆的圆心P到两定点A（-3，0）和定圆的圆心B（3，0）的距离之和恰好等于定圆半径，属于中档题．
练习册系列答案
中考解读考点精练系列答案
相关题目
已知动圆P过定点A（-3，0），并且在定圆B：（x-3）2+y2=64的内部与其相内切，求动圆圆心P的轨迹方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
