题目内容
已知圆C同时满足下列三个条件:①圆心在直线x-3y=0上;
②与y轴相切;③在x轴上截得的弦长AB为42.求圆C的一般方程.
圆的一般方程为x2+y2+6x+2y+1=0或x2+y2-6x-2y+1=0.
解析:
设所求圆的方程为x2+y2+Dx+Ey+F=0,则圆心为![]() ,半径
,半径![]() 为,
为,
∵圆心在直线x-3y=0上,∴![]() ,即D=3E.①
,即D=3E.①
又∵圆与y轴相切,∴![]() ,即E2-4F=0.②
,即E2-4F=0.②
圆的方程中令y=0,得x2+Dx+F=0,
设A(x1,0),B(x2,0),
依题意|x1-x2|=42即(x1-x2)2=32,∴(x1+x2)2-4x1x2=32.∴D2-4F=32.③
由①②③解得D=6,E=2,F=1或D=-6,E=-2, F=1,?
故所求圆的一般方程为x2+y2+6x+2y+1=0或x2+y2-6x-2y+1=0.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
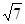 ;③圆心在直线x-3y=0上. 求圆C的方程.
;③圆心在直线x-3y=0上. 求圆C的方程. 上截得弦长为2
上截得弦长为2 ;③圆心在直线
;③圆心在直线 上,求圆C的方程.
上,求圆C的方程.