题目内容
(12分)如图,已知圆C:![]() ,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足![]() =
=![]() ,
,![]() ?
?![]() =0,点N的轨迹为曲线E.
=0,点N的轨迹为曲线E.
(Ⅰ)求曲线E的方程;
(Ⅱ)若过定点A(1,0)的直线![]() 交曲线E于不同的两点G、H,
交曲线E于不同的两点G、H,
且满足∠GOH为锐角,求直线![]() 的斜率k的取值范围.
的斜率k的取值范围.

解析:(Ⅰ)依题PN为AM的中垂线
![]()
![]() ……………………………………2分
……………………………………2分
又C(-1,0),A(1,0)
所以N的轨迹E为椭圆,C、A为其焦点………………………………4分
a=![]() ,c=1,所以
,c=1,所以![]() 为所求…………………………………5分
为所求…………………………………5分
(Ⅱ)设直线![]() 的方程为:y=k(x-1)代入椭圆方程:x2+2y2=2得
的方程为:y=k(x-1)代入椭圆方程:x2+2y2=2得
(1+2k2)x2-4k2x+2k2-2=0………………(1)
设G(x1,y1)、H(x2,y2),则x1,x2是(1)的两个根.
![]() ……………………………………7分
……………………………………7分
依题![]()
![]()
![]()
![]() ………………………………………9分
………………………………………9分
解得:![]() ……………………………………………………12分
……………………………………………………12分

练习册系列答案
相关题目
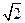 ,AF=1,M是线段EF的中点。
,AF=1,M是线段EF的中点。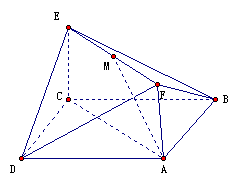
 的底面是正方形,
的底面是正方形, ,且
,且 ,点
,点 分别在侧棱
分别在侧棱 、
、 上,且
上,且 。
。
 ;
; ,求平面
,求平面 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值. 的底面是正方形,
的底面是正方形,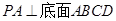 ,且
,且 ,点
,点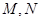 分别在侧棱
分别在侧棱 、
、 上,且
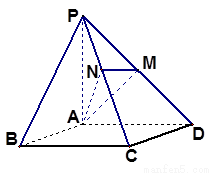
上,且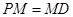 。
。
 ;
; ,求平面
,求平面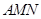 与平面
与平面 所成二面角的余弦值.
所成二面角的余弦值.  中,
中, ,
, 平面
平面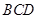 ,
,
 分别为
分别为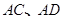 上的动点.
上的动点.  ,求证:平面
,求证:平面 平面
平面 ;
; ,
, ,求平面
,求平面 与平面
与平面
 的大小。
的大小。