题目内容
己知斜率为1的直线l与双曲线C: 相交于B、D两点,且BD的中点为M(1,3).
相交于B、D两点,且BD的中点为M(1,3).(Ⅰ)求C的离心率;
(Ⅱ)设C的右顶点为A,右焦点为F,|DF|•|BF|=17,证明:过A、B、D三点的圆与x轴相切.
【答案】分析:(Ⅰ)由直线过点(1,3)及斜率可得直线方程,直线与双曲线交于BD两点的中点为(1,3),可利用直线与双曲线消元后根据中点坐标公式找出a,b的关系式即求得离心率.
(Ⅱ)利用离心率将条件|FA||FB|=17,用含a的代数式表示,即可求得a,则A点坐标可得(1,0),由于A在x轴上所以,只要证明2AM=BD即证得.
解答: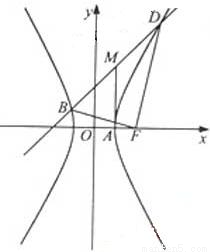 解:(Ⅰ)由题设知,l的方程为:y=x+2,代入C的方程,并化简,
解:(Ⅰ)由题设知,l的方程为:y=x+2,代入C的方程,并化简,
得(b2-a2)x2-4a2x-a2b2-4a2=0,
设B(x1,y1),D(x2,y2),则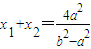 ,
,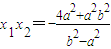 ,①
,①
由M(1,3)为BD的中点知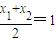 .
.
故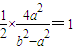 ,即b2=3a2,②
,即b2=3a2,②
故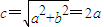 ,
,
∴C的离心率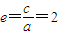 .
.
(Ⅱ)由①②知,C的方程为:3x2-y2=3a2,A(a,0),F(2a,0),
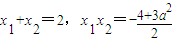 .
.
故不妨设x1≤-a,x2≥a,
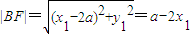 ,
,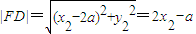 ,
,
|BF|•|FD|=(a-2x1)(2x2-a)=-4x1x2+2a(x1+x2)-a2=5a2+4a+8.
又|BF|•|FD|=17,故5a2+4a+8=17.
解得a=1,或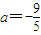 (舍去),
(舍去),
故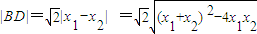 =6,
=6,
连接MA,则由A(1,0),M(1,3)知|MA|=3,
从而MA=MB=MD,且MA⊥x轴,
因此以M为圆心,MA为半径的圆经过A、B、D三点,且在点A处与x轴相切,
所以过A、B、D三点的圆与x轴相切.
点评:本题考查了圆锥曲线、直线与圆的知识,考查学生运用所学知识解决问题的能力.
(Ⅱ)利用离心率将条件|FA||FB|=17,用含a的代数式表示,即可求得a,则A点坐标可得(1,0),由于A在x轴上所以,只要证明2AM=BD即证得.
解答:
 解:(Ⅰ)由题设知,l的方程为:y=x+2,代入C的方程,并化简,
解:(Ⅰ)由题设知,l的方程为:y=x+2,代入C的方程,并化简,得(b2-a2)x2-4a2x-a2b2-4a2=0,
设B(x1,y1),D(x2,y2),则
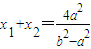 ,
,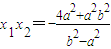 ,①
,①由M(1,3)为BD的中点知
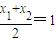 .
.故
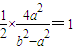 ,即b2=3a2,②
,即b2=3a2,②故
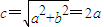 ,
,∴C的离心率
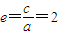 .
.(Ⅱ)由①②知,C的方程为:3x2-y2=3a2,A(a,0),F(2a,0),
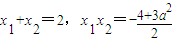 .
.故不妨设x1≤-a,x2≥a,
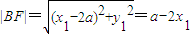 ,
,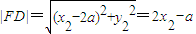 ,
,|BF|•|FD|=(a-2x1)(2x2-a)=-4x1x2+2a(x1+x2)-a2=5a2+4a+8.
又|BF|•|FD|=17,故5a2+4a+8=17.
解得a=1,或
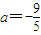 (舍去),
(舍去),故
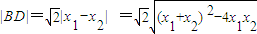 =6,
=6,连接MA,则由A(1,0),M(1,3)知|MA|=3,
从而MA=MB=MD,且MA⊥x轴,
因此以M为圆心,MA为半径的圆经过A、B、D三点,且在点A处与x轴相切,
所以过A、B、D三点的圆与x轴相切.
点评:本题考查了圆锥曲线、直线与圆的知识,考查学生运用所学知识解决问题的能力.

练习册系列答案
相关题目
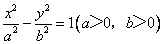 相交于B、D两点,且BD的中点为
相交于B、D两点,且BD的中点为 .
. ,证明:过A、B、D三点的圆与x轴相切.
,证明:过A、B、D三点的圆与x轴相切.