题目内容
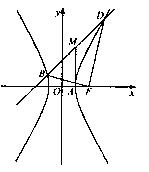
己知斜率为1的直线l与双曲线C: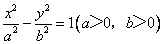 相交于B、D两点,且BD的中点为
相交于B、D两点,且BD的中点为 .
.
(Ⅰ)求C的离心率;
(Ⅱ)设C的右顶点为A,右焦点为F, ,证明:过A、B、D三点的圆与x轴相切.
,证明:过A、B、D三点的圆与x轴相切.
【答案】
【命题意图】本题主要考查双曲线的方程及性质,考查直线与圆的关系,既考查考生的基础知识掌握情况,又可以考查综合推理的能力.
【参考答案】
(I)由题设知,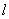 的方程为
的方程为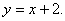
代入C的方程,并化简得,
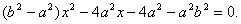
设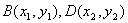
则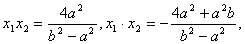 ①
①
由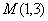 为B D的中点知
为B D的中点知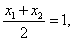 故
故
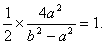
即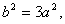 ②
②
故
所以C的离心率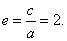
(II)由①、②知,C的方程为: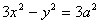
A(a,0),F(2a,0),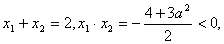
故不妨设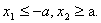
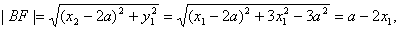
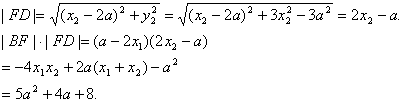
又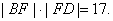
 故
故
解得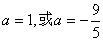 (舍去)
(舍去)
故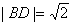

连结MA,则由A(1,0),M(1,3)知|MA|=3,从而
MA=MB=MD,且MA⊥x轴,因此以M为圆主,MA
为半径的圆经地A、B、D三点,且在点A处与x轴相切,
所以过A、B、D三点的圆与x轴相切。
【点评】高考中的解析几何问题一般为综合性较强的题目,命题者将好多考点以圆锥曲线为背景来考查,如向量问题、三角形问题、函数问题等等,试题的难度相对比较稳定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 相交于B、D两点,且BD的中点为M(1,3).
相交于B、D两点,且BD的中点为M(1,3).