题目内容
已知向量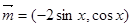 ,
,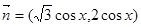 ,函数
,函数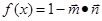
(1)求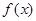 的最小正周期; (2)当
的最小正周期; (2)当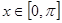 时,求
时,求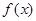 的单调递增区间;
的单调递增区间;
(3)说明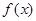 的图像可以由
的图像可以由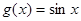 的图像经过怎样的变换而得到。
的图像经过怎样的变换而得到。
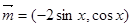 ,
,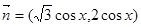 ,函数
,函数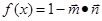
(1)求
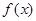 的最小正周期; (2)当
的最小正周期; (2)当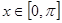 时,求
时,求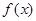 的单调递增区间;
的单调递增区间;(3)说明
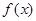 的图像可以由
的图像可以由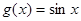 的图像经过怎样的变换而得到。
的图像经过怎样的变换而得到。(1) ;
;
(2)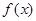 的递增区间为
的递增区间为 和
和 ;
;
(3)将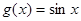 的图像向右平移
的图像向右平移 ,再保持纵坐标不变,横坐标缩短为原来的
,再保持纵坐标不变,横坐标缩短为原来的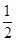 ;再保持横坐标不变,纵坐标变为2倍即得
;再保持横坐标不变,纵坐标变为2倍即得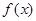 的图像。
的图像。
 ;
; (2)
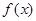 的递增区间为
的递增区间为 和
和 ;
;(3)将
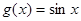 的图像向右平移
的图像向右平移 ,再保持纵坐标不变,横坐标缩短为原来的
,再保持纵坐标不变,横坐标缩短为原来的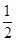 ;再保持横坐标不变,纵坐标变为2倍即得
;再保持横坐标不变,纵坐标变为2倍即得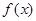 的图像。
的图像。本试题主要是考查了三角函数的图像与性质的运用。
(1)因为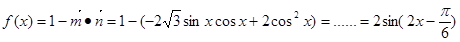 ,那么利用周期公式得到。
,那么利用周期公式得到。
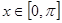 时,
时,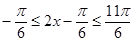
 ;
;
当 和
和 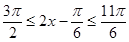 时,即
时,即 和
和  时,函数递增。从而得到单调区间。
时,函数递增。从而得到单调区间。
(2)利用三角函数图像的变换得到结论
(1)因为
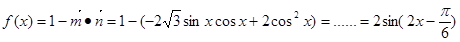 ,那么利用周期公式得到。
,那么利用周期公式得到。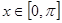 时,
时,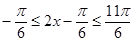
 ;
;当
 和
和 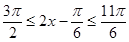 时,即
时,即 和
和  时,函数递增。从而得到单调区间。
时,函数递增。从而得到单调区间。(2)利用三角函数图像的变换得到结论

练习册系列答案
相关题目
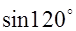 =( )
=( )



 +
+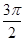 )(x∈[0,2π])的图象和直线y=
)(x∈[0,2π])的图象和直线y= 的交点个数是( )
的交点个数是( ) 的终边上有一点
的终边上有一点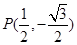 ,求
,求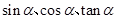 的值;
的值;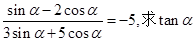 的值。
的值。 的部分图象如左下图所示,则
的部分图象如左下图所示,则
 的值分别为 .
的值分别为 .
 的单调增区间是
的单调增区间是
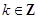



 ,
, ,则
,则 ( )
( ) 



 ,
, ,则
,则 。
。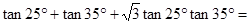 ______________________.
______________________.