题目内容
已知函数 .
.
(Ⅰ)求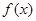 的单调减区间;
的单调减区间;
(Ⅱ)求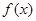 在区间
在区间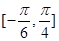 上最大值和最小值.
上最大值和最小值.
【答案】
(Ⅰ)函数的单调减区间是: ;(Ⅱ)
;(Ⅱ)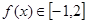 .
.
【解析】
试题分析:(Ⅰ)将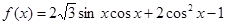 降次化一,化为
降次化一,化为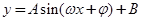 的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.
的形式,然后利用正弦函数的单调区间,即可求得其单调递增区间.
(Ⅱ)由(Ⅰ)可得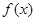
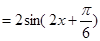 ,又
,又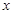 的范围为
的范围为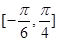 ,由此可得
,由此可得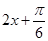 的范围,进而求得
的范围,进而求得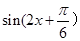 的范围.
的范围.
试题解析: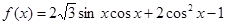
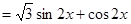
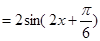 .
.
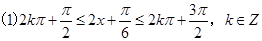
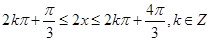
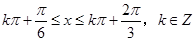
函数的单调减区间是:  .
.
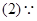
 的范围为
的范围为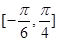 ,所以
,所以 ,
,
所以 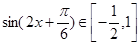
即: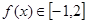
考点:1、三角恒等变换;2、三角函数的单调区间及范围.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.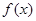 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求