题目内容
已知(2－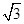
x)50＝a0＋a1x＋a2x2＋…＋a50x50，其中a0，a1，a2…，a50是常数，计算(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2.
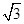x)50＝a0＋a1x＋a2x2＋…＋a50x50，其中a0，a1，a2…，a50是常数，计算(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2.1
设f(x)＝(2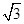－x)50，
令x＝1，得a0＋a1＋a2＋…＋a50＝(2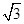－)50，令x＝－1，得a0－a1＋a2－…＋a50＝(2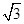＋)50，
(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2＝(a0＋a1＋a2＋…＋a50)(a0－a1＋a2－…＋a50)
＝(2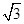－)50(2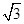＋)50＝1.
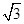x)50，令x＝1，得a0＋a1＋a2＋…＋a50＝(2－
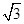)50，令x＝－1，得a0－a1＋a2－…＋a50＝(2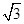＋)50，(a0＋a2＋a4＋…＋a50)2－(a1＋a3＋a5＋…＋a49)2＝(a0＋a1＋a2＋…＋a50)(a0－a1＋a2－…＋a50)
＝(2－
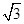)50(2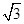＋)50＝1.
练习册系列答案
相关题目
的二项展开式的第三项为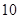
，则
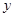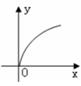
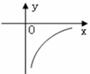
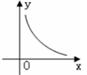
关于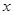
的函数图像大致形状为（ ）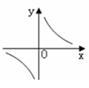
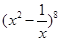的展开式中，含
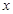的项的系数是________
10展开式中的常数项．
，
,
,则
的值为__ ___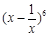
的展开式的中间一项是__________．
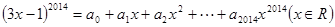，则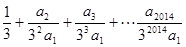
= .