题目内容
设函数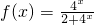 ,
,
(1)用定义证明:函数f(x)是R上的增函数;
(2)证明:对任意的实数t,都有f(t)+f(1-t)=1;
(3)求值: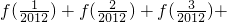 …
…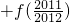 .
.
解:(1)证明:设任意x1<x2,
则f(x1)-f(x2)=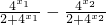 =
=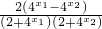 ,
,
∵x1<x2,
∴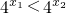 ,∴
,∴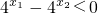 ,
,
又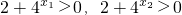 .
.
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),…(4分)
∴f(x)在R上是增函数 …(6分)
(2)对任意t,f(t)+f(1-t)=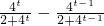 =
=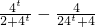 =
=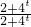 =1.
=1.
∴对于任意t,f(t)+f(1-t)=1 …(10分)
(3)∵由(2)得f(t)+f(1-t)=1
∴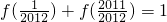 ,
,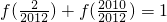 ,
,
∴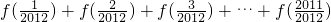 +
+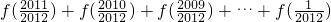 =2011,
=2011,
∴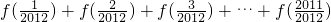 =
=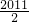 …(14分)
…(14分)
分析:(1)直接利用用定义,通过f(x1)-f(x2)化简表达式,比较出大小即可证明函数f(x)是R上的单调性;
(2)化简f(t)+f(1-t),证明它的值是1即可;
(3)由(2),f(t)+f(1-t)=1,求出首末两项的和为1,利用倒序相加法,求出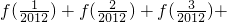 …
…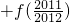 .
.
点评:本题考查函数的单调性的证明,函数值的求法,考查计算能力,值域倒序相加法的应用.
则f(x1)-f(x2)=
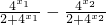 =
=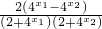 ,
,∵x1<x2,
∴
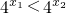 ,∴
,∴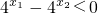 ,
,又
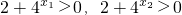 .
.∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),…(4分)
∴f(x)在R上是增函数 …(6分)
(2)对任意t,f(t)+f(1-t)=
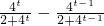 =
=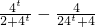 =
=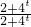 =1.
=1.∴对于任意t,f(t)+f(1-t)=1 …(10分)
(3)∵由(2)得f(t)+f(1-t)=1
∴
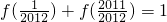 ,
,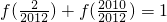 ,
,∴
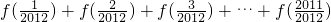 +
+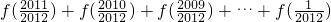 =2011,
=2011,∴
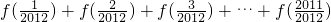 =
=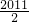 …(14分)
…(14分)分析:(1)直接利用用定义,通过f(x1)-f(x2)化简表达式,比较出大小即可证明函数f(x)是R上的单调性;
(2)化简f(t)+f(1-t),证明它的值是1即可;
(3)由(2),f(t)+f(1-t)=1,求出首末两项的和为1,利用倒序相加法,求出
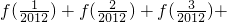 …
…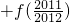 .
.点评:本题考查函数的单调性的证明,函数值的求法,考查计算能力,值域倒序相加法的应用.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目