题目内容
投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机散一粒豆子,求豆子落在区域M上的概率.
【答案】
(1)以0,2,4为横、纵坐标的点P的可能共3×3=9个,
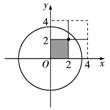
而这些点中,落在区域C的点有:(0,0)、(0,2)、(2,0)、(2,2)4个 ,
∴所求概率为P=.
(2)∵区域M的面积为4,而区域C的面积为10π,
∴所求概率P==.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的横坐标和纵坐标.
的横坐标和纵坐标.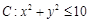 内的概率;
内的概率;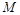 ,在区域
,在区域 上随机撒一粒豆子,求豆子落在区域
上随机撒一粒豆子,求豆子落在区域