题目内容
投掷一个质地均匀的、每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面出现的数字分别作为点P的横坐标和纵坐标(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
分析:(1)本小题是古典概型问题,欲求出点P落在区域C:x2+y2≤10内的概率,只须求出满足:x2+y2≤10上的点P的坐标有多少个,再将求得的值与整个点P的坐标个数求比值即得.
(2)本小题是几何概型问题,欲求豆子落在区域M上的概率,只须求出满足:“豆子落在区域M上的概率”的区域的面积,再将求得的面积值与整个区域C的面积求比值即得.
(2)本小题是几何概型问题,欲求豆子落在区域M上的概率,只须求出满足:“豆子落在区域M上的概率”的区域的面积,再将求得的面积值与整个区域C的面积求比值即得.
解答: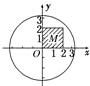 解:(1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),
解:(1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),
(4,2),(4,4),共9种,其中落在区域C:x2+y2≤10上的点P的坐标有:
(0,0),(0,2),(2,0),(2,2),共4种D、故点P落在区域C:x2+y2≤10内的
概率为
.
(2)区域M为一边长为2的正方形,其面积为4,区域C的面积为10π,则豆子落在区域M上的概率为
.
 解:(1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),
解:(1)点P的坐标有:(0,0),(0,2),(0,4),(2,0),(2,2),(2,4),(4,0),(4,2),(4,4),共9种,其中落在区域C:x2+y2≤10上的点P的坐标有:
(0,0),(0,2),(2,0),(2,2),共4种D、故点P落在区域C:x2+y2≤10内的
概率为
| 4 |
| 9 |
(2)区域M为一边长为2的正方形,其面积为4,区域C的面积为10π,则豆子落在区域M上的概率为
| 2 |
| 5π |
点评:本小题主要考查古典概型、几何概型等基础知识.古典概型与几何概型的主要区别在于:几何概型是另一类等可能概型,它与古典概型的区别在于试验的结果是不是有限个,
几何概型的特点有下面两个:(1)试验中所有可能出现的基本事件有无限多个.(2)每个基本事件出现的可能性相等.
几何概型的特点有下面两个:(1)试验中所有可能出现的基本事件有无限多个.(2)每个基本事件出现的可能性相等.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 的横坐标和纵坐标.
的横坐标和纵坐标.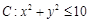 内的概率;
内的概率; ,在区域
,在区域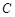 上随机撒一粒豆子,求豆子落在区域
上随机撒一粒豆子,求豆子落在区域