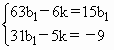题目内容
以数列{an}的任意相邻两项为坐标的点Pn(an，an+1)(n∈N)均在一次函数y＝2x＋k的图象上，数列{bn}满足条件：bn＝an+1－an(n∈N，b1≠0)，
(1)求证：数列{bn}是等比数列；
(2)设数列{an}，{bn}的前n项和分别为Sn，Tn，若S6＝T4，S5＝－9，求k的值．
答案：
解析：
解析：
|
解：(1)依题意 ∴ ∴ ∵ ∴数列{ (2)由(1)得 又由(1)中的(*)式得： ∴ 由 得： 解得： |
，
，(*)
，
，∴
．
}是以b1为首项，2为公比的等比数列．
，
，
，
，
，
．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目