题目内容
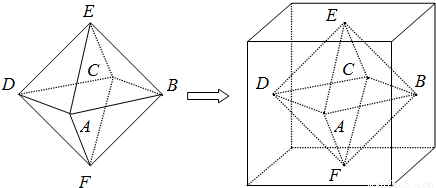
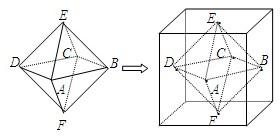
两个相同的正四棱锥底面重合组成一个八面体,可放于棱长为1的正方体中,重合的底面与正方体的某一个面平行,各顶点均在正方体的表面上,把满足上述条件的八面体称为正方体的“正子体”.(1)若正子体的六个顶点分别是正方体各面的中心,求异面直线DE与CF所成的角;
(2)问此正子体的体积V是否为定值?若是,求出该定值;若不是,求出体积大小的取值范围.
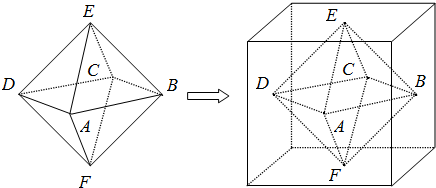
分析:(1)求异面直线所成的角可以建立坐标系来解,分别以CA、DB为x、y轴建立空间直角坐标系,根据几何体的长度写出要用的点的坐标,写出两条异面直线对应的向量,根据异面直线所成角为锐角,得到异面直线DE与CF所成的角.
(2)正子体体积不是定值.把正子体分成两个四棱锥,分别求两个四棱锥的体积,根据底面的范围,得到正子体的体积在一个取值范围中,不是一个定值.
(2)正子体体积不是定值.把正子体分成两个四棱锥,分别求两个四棱锥的体积,根据底面的范围,得到正子体的体积在一个取值范围中,不是一个定值.
解答:解:(1)分别以CA、DB为x、y轴建立空间直角坐标系.
因为AC=1,BD=1,
∴D(0,-
,0),E(0,0,
),C(-
,0,0),
F(0,0,-
),
={0,
,
},
={
,0,-
}
cosθ=-
因为异面直线所成角为锐角,
故异面直线DE与CF所成的角为60°
(2)正子体体积不是定值.
设ABCD与正方体的截面四边形为A′B′C′D′,
设AA′=x(0≤x≤1),则AB′=1-x
|AD|2=x2+(1-x)2=2(x-
)2+
故SABCD=|AD|2∈[
,1]
V=
•SABCD•h•2=
•SABCD•
•2=
SABCD∈[
,
].
因为AC=1,BD=1,
∴D(0,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
F(0,0,-
| 1 |
| 2 |
| DE |
| 1 |
| 2 |
| 1 |
| 2 |
| CF |
| 1 |
| 2 |
| 1 |
| 2 |
cosθ=-
| 1 |
| 2 |
因为异面直线所成角为锐角,
故异面直线DE与CF所成的角为60°
(2)正子体体积不是定值.
设ABCD与正方体的截面四边形为A′B′C′D′,
设AA′=x(0≤x≤1),则AB′=1-x
|AD|2=x2+(1-x)2=2(x-
| 1 |
| 2 |
| 1 |
| 2 |
故SABCD=|AD|2∈[
| 1 |
| 2 |
V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |

点评:本题考查简单组合体的体积,考查几何体的结构特征,考查异面直线所成的角,本题是一个综合题目,需要注意数据的运算不要出错.

练习册系列答案
相关题目
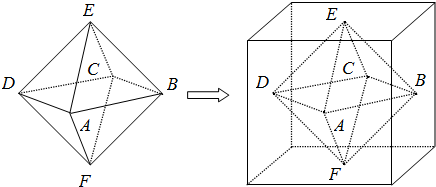
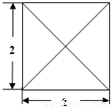
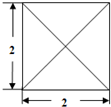 把两个相同的正四棱锥底面重叠在一起,恰好得到一个正八面体,若该正八面体的俯视图如图所示,则它的主视图面积为( )
把两个相同的正四棱锥底面重叠在一起,恰好得到一个正八面体,若该正八面体的俯视图如图所示,则它的主视图面积为( )