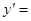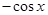题目内容
已知函数f(x)=aln x= (a为常数).
(a为常数).
(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
 (a为常数).
(a为常数).(1)若曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,求a的值;
(2)求函数f(x)的单调区间;
(3)当x≥1时,f(x)≤2x-3恒成立,求a的取值范围.
(1)a=1(2)f(x)的单调增区间为(0,+∞),单调减区间为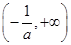 (3)a≤1.
(3)a≤1.
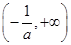 (3)a≤1.
(3)a≤1.(1)函数f(x)的定义域为{x|x>0},f′(x)=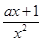 .
.
又曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,
所以f′(1)=a+1=2,即a=1.(4分)
(2)由f′(x)=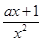 (x>0),
(x>0),
当a≥0时,
f′(x)>0恒成立,所以f(x)的单调增区间为(0,+∞).
当a<0时,
由f′(x)>0,得0<x<-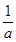 ,
,
所以f(x)的单调增区间为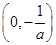 ;
;
由f′(x)<0,得x>-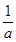 ,
,
所以f(x)的单调减区间为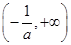 .(10分)
.(10分)
(3)设g(x)=aln x- -2x+3,x∈[1,+∞),
-2x+3,x∈[1,+∞),
则g′(x)=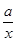 +
+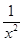 -2=
-2=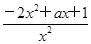 .
.
令h(x)=-2x2+ax+1,考虑到h(0)=1>0,
当a≤1时,
h(x)=-2x2+ax+1的对称轴x=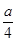 <1,
<1,
h(x)在[1,+∞)上是减函数,h(x)≤h(1)=a-1≤0,
所以g′(x)≤0,g(x)在[1,+∞)上是减函数,
所以g(x)≤g(1)=0,即f(x)≤2x2-3恒成立.
当a>1时,
令h(x)=-2x2+ax+1=0,
得x1=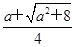 >1,x2=
>1,x2=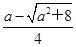 <0,
<0,
当x∈[1,x1)时,h(x)>0,即g′(x)>0,
g(x)在[1,x1)上是增函数;
当x∈(x1,+∞)时,h(x)<0,即g′(x)<0,
g(x)在(x1,+∞)上是减函数.
所以0=g(1)<g(x1),即f(x1)>2x1-3,不满足题意.
综上,a的取值范围为a≤1.(16分)
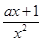 .
.又曲线y=f(x)在点(1,f(1))处的切线与直线x+2y-5=0垂直,
所以f′(1)=a+1=2,即a=1.(4分)
(2)由f′(x)=
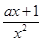 (x>0),
(x>0),当a≥0时,
f′(x)>0恒成立,所以f(x)的单调增区间为(0,+∞).
当a<0时,
由f′(x)>0,得0<x<-
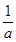 ,
,所以f(x)的单调增区间为
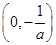 ;
;由f′(x)<0,得x>-
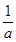 ,
,所以f(x)的单调减区间为
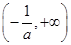 .(10分)
.(10分)(3)设g(x)=aln x-
 -2x+3,x∈[1,+∞),
-2x+3,x∈[1,+∞),则g′(x)=
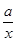 +
+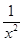 -2=
-2=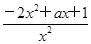 .
.令h(x)=-2x2+ax+1,考虑到h(0)=1>0,
当a≤1时,
h(x)=-2x2+ax+1的对称轴x=
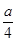 <1,
<1,h(x)在[1,+∞)上是减函数,h(x)≤h(1)=a-1≤0,
所以g′(x)≤0,g(x)在[1,+∞)上是减函数,
所以g(x)≤g(1)=0,即f(x)≤2x2-3恒成立.
当a>1时,
令h(x)=-2x2+ax+1=0,
得x1=
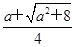 >1,x2=
>1,x2=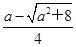 <0,
<0,当x∈[1,x1)时,h(x)>0,即g′(x)>0,
g(x)在[1,x1)上是增函数;
当x∈(x1,+∞)时,h(x)<0,即g′(x)<0,
g(x)在(x1,+∞)上是减函数.
所以0=g(1)<g(x1),即f(x1)>2x1-3,不满足题意.
综上,a的取值范围为a≤1.(16分)

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

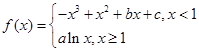 的图像过坐标原点
的图像过坐标原点 ,且在点
,且在点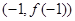 处的切线的斜率是
处的切线的斜率是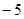 .
.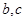 的值;
的值;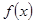 在区间
在区间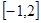 上的最大值;
上的最大值;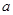 ,曲线
,曲线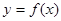 上是否存在两点
上是否存在两点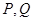 ,使得
,使得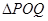 是以
是以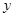 轴上?请说明理由.
轴上?请说明理由.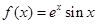 函数.
函数.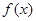 单调递增区间;
单调递增区间;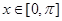 时,求函数
时,求函数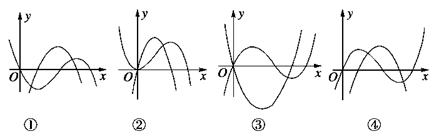
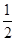 mx2+ln x-2x在定义域内是增函数,则实数m的取值范围是________.
mx2+ln x-2x在定义域内是增函数,则实数m的取值范围是________.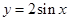 的导数
的导数