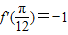题目内容
以下命题正确的是
（1）把函数y=3sin（2x+
）的图象向右平移
个单位得到y=3sin2x的图象．
（2）若等差数列的前n项和为Sn则三点（(10，
)，(100，
)，(110，
)共线
（3）若f（x）=cos4x-sin4x则f′(
)=-1
（4）若三次函数f（x）=ax3+bx2+cx+d则“a+b+c=0”是f（x）有极值点的充要条件．
（1）（2）（3）
（1）（2）（3）
（1）把函数y=3sin（2x+
| π |
| 3 |
| π |
| 6 |
（2）若等差数列的前n项和为Sn则三点（(10，
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
（3）若f（x）=cos4x-sin4x则f′(
| π |
| 12 |
（4）若三次函数f（x）=ax3+bx2+cx+d则“a+b+c=0”是f（x）有极值点的充要条件．
分析：（1）利用三角函数的平移变换规律（左加右减）即可判断其正误；
（2）等差数列中
=a1+（n-1）•
，由此可判断三点（(10，
)，(100，
)，(110，
)共线；
（3）f（x）=cos4x-sin4x=cos2x，f′（x）=-2sin2x，从而可判断其正误；
（4）f（x）=ax3+bx2+cx+d有极值⇒f′（x）=3ax2+2bx+c=0有解，不能推出a+b+c=0，从而可否定（4）．
（2）等差数列中
| Sn |
| n |
| d |
| 2 |
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
（3）f（x）=cos4x-sin4x=cos2x，f′（x）=-2sin2x，从而可判断其正误；
（4）f（x）=ax3+bx2+cx+d有极值⇒f′（x）=3ax2+2bx+c=0有解，不能推出a+b+c=0，从而可否定（4）．
解答：解：（1）y=3sin（2x+
）
y=3sin[2（x-
）+
]=3sin2x，故（1）正确；
（2）∵{an}为等差数列，设其公差为d，依题意得，
=a1+（n-1）•
，即
为n的线性函数，故（10，
），（100，
），（110，
）三点共线，故（2）正确；
（3）∵f（x）=cos4x-sin4x=cos2x-sin2x=cos2x，
∴f′（x）=-2sin2x，
∴f′（
）=-2sin（2×
）=-1，故（3）正确；
对于（4），f（x）=ax3+bx2+cx+d有极值⇒f′（x）=3ax2+2bx+c=0有解，不能推出a+b+c=0，故（4）错误．
故命题正确的是（1），（2），（3）．
故答案为：（1），（2），（3）．
| π |
| 3 |
图象向右平移
| ||
| π |
| 6 |
| π |
| 3 |
（2）∵{an}为等差数列，设其公差为d，依题意得，
| Sn |
| n |
| d |
| 2 |
| Sn |
| n |
| S10 |
| 10 |
| S100 |
| 100 |
| S110 |
| 110 |
（3）∵f（x）=cos4x-sin4x=cos2x-sin2x=cos2x，
∴f′（x）=-2sin2x，
∴f′（
| π |
| 12 |
| π |
| 12 |
对于（4），f（x）=ax3+bx2+cx+d有极值⇒f′（x）=3ax2+2bx+c=0有解，不能推出a+b+c=0，故（4）错误．
故命题正确的是（1），（2），（3）．
故答案为：（1），（2），（3）．
点评：本题考查函数y=Asin（ωx+φ）的图象变换，考查等差数列的性质，命题的真假判断与应用，考查必要条件、充分条件与充要条件的判断及导数的运算与应用，综合性强，属于中档题．
练习册系列答案
相关题目
）的图象向右平移
个单位得到y=3sin2x的图象．
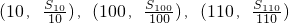共线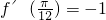
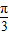）的图象向右平移
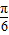个单位得到y=3sin2x的图象．
共线