题目内容
以下命题正确的是
(1)若log23=a,则log218=1+2a;
(2)若A={x|(2+x)(2-x)>0},{x|log2x<1},则x∈A是x∈B必要非充分条件;
(3)函数y=sin2x+
的值域是[4,+∞);
(4)若奇函数f(x)满足f(2+x)=-f(x),则函数图象关于直线x=2对称.
(1)(2)
(1)(2)
(1)若log23=a,则log218=1+2a;
(2)若A={x|(2+x)(2-x)>0},{x|log2x<1},则x∈A是x∈B必要非充分条件;
(3)函数y=sin2x+
| 4 | sin2x |
(4)若奇函数f(x)满足f(2+x)=-f(x),则函数图象关于直线x=2对称.
分析:(1)由log218=log22+2log23,利用log23=a能得到(1)正确;
(2)由A={x|(2+x)(2-x)>0}={x|-2<x<2},B={x|log2x<1}={x|x<2},能得到(2)正确;
(3)函数y=sin2x+
≥2
=4的前提条件是sin2x=2,由sin2x∈[0,1],知(3)不正确;
(4)由f(1+x)=-f(x),能导出f(x)的图象关于直线x=
对称,故(4)不正确.
(2)由A={x|(2+x)(2-x)>0}={x|-2<x<2},B={x|log2x<1}={x|x<2},能得到(2)正确;
(3)函数y=sin2x+
| 4 |
| sin2x |
sin2x•
|
(4)由f(1+x)=-f(x),能导出f(x)的图象关于直线x=
| 1 |
| 2 |
解答:解:(1)∵log23=a,∴log218=log22+2log23=1+2a,故(1)正确;
(2)∵A={x|(2+x)(2-x)>0}={x|-2<x<2},B={x|log2x<1}={x|x<2},
∴x∈A是x∈B必要非充分条件,故(2)正确;
(3)函数y=sin2x+
≥2
=4的前提条件是sin2x=2,
∵sin2x∈[0,1],∴函数y=sin2x+
的值域不是[4,+∞),故(3)不正确;
(4)∵f(1+x)=-f(x)
∴f(x+
)=f(x-
+1)=-f(x-
)=f(
-x)
∴f(x)的图象关于直线x=
对称,故(4)不正确.
故答案为:(1),(2).
(2)∵A={x|(2+x)(2-x)>0}={x|-2<x<2},B={x|log2x<1}={x|x<2},
∴x∈A是x∈B必要非充分条件,故(2)正确;
(3)函数y=sin2x+
| 4 |
| sin2x |
sin2x•
|
∵sin2x∈[0,1],∴函数y=sin2x+
| 4 |
| sin2x |
(4)∵f(1+x)=-f(x)
∴f(x+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)的图象关于直线x=
| 1 |
| 2 |
故答案为:(1),(2).
点评:本题考查命题的真假判断与应用,是基础题.解题时要认真审题,仔细解答.注意对数性质、集合、均值不等式、对称性的灵活运用.

练习册系列答案
相关题目
 )的图象向右平移
)的图象向右平移 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象. 共线
共线
 )的图象向右平移
)的图象向右平移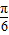 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象. 共线
共线