题目内容
9.设全集U={x|x≤5且x∈N*},集合A={x|x2-7x+q=0},B={x|x2+px+12=0},且(∁UA )∪B={1,2,3,4,5},求实数p、q的值.分析 根据集合的基本运算,转化为根与系数之间的关系,进行求解即可.
解答 解:∵U={x|x≤5且x∈N*}={1,2,3,4,5},(∁UA )∪B={1,2,3,4,5},
∴A=B,且方程x2-7x+q=0与x2+px+12=0为同解方程,且方程有两个相同的根,
则p=-7,q=12,
设A=B={a,b},
则a+b=7,ab=12,
解得a=3,b=4或a=4,b=3,即A=B={3,4},
则满足(∁UA )∪B={1,2,3,4,5},
即p=-7,q=12.
点评 本题主要考查集合的基本运算,根据条件转化为一元二次方程根与系数之间的关系是解决本题的关键.

练习册系列答案
相关题目
20.已知函数f(x)=$\frac{1}{2}$sin(2x+$\frac{π}{6}$),若f(x-φ)为偶函数,则φ可以为( )
| A. | $\frac{π}{2}$ | B. | -$\frac{π}{3}$ | C. | -$\frac{π}{6}$ | D. | $\frac{π}{6}$ |
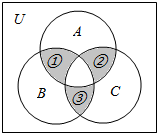 如图所示,已知全集U,用集合A、B、C及其交集、并集、补集的运算表示出图中的阴影部分.
如图所示,已知全集U,用集合A、B、C及其交集、并集、补集的运算表示出图中的阴影部分.