题目内容
设集合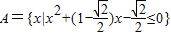 ,
,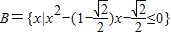 ,又设函数f(x)=2x2+mx-1.
,又设函数f(x)=2x2+mx-1.(1)若不等式f(x)≤0的解集为C,且C⊆(A∪B),求实数m的取值范围.
(2)若对任意x∈R,有f(1-x)=f(1+x)成立,试求当x∈(A∩B)时,函数f(x)的值域.
(3)当m∈(A∪B),x∈(A∩B)时,求证:
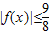 .
.
【答案】分析:(1)先分别化简集合A,B,可求A∪B=[-1,1],要使C⊆(A∪B),则 ,故得解;
,故得解;
(2)先求得) ,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域.
,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域.
(3)m∈[-1,1],x∈ ,从而f(x)的最小值为-1,最大值在端点处取得,故可证.
,从而f(x)的最小值为-1,最大值在端点处取得,故可证.
解答:解:(1)由题意, ,
,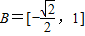
∴A∪B=[-1,1]
要使C⊆(A∪B),则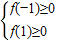
∴实数m的取值范围是m≥-1.
(2)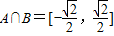
∵对任意x∈R,有f(1-x)=f(1+x)成立,
∴函数的对称轴为x=1
∴m=-4
∴f(x)=2x2-4x-1=2(x-1)2-3.
∵x∈(A∩B),
∴函数f(x)的值域为 .
.
(3)m∈[-1,1],x∈
∴f(x)的最小值为-1,最大值在端点处取得
∵

∴
点评:本题以集合为载体,考查函数值域,考查函数的最值,关键是集合的化简.
 ,故得解;
,故得解;(2)先求得)
 ,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域.
,由于对任意x∈R,有f(1-x)=f(1+x)成立,可知函数的对称轴为x=1,从而可确定函数f(x)=2x2-4x-1=2(x-1)2-3.,进而可求函数f(x)的值域.(3)m∈[-1,1],x∈
 ,从而f(x)的最小值为-1,最大值在端点处取得,故可证.
,从而f(x)的最小值为-1,最大值在端点处取得,故可证.解答:解:(1)由题意,
 ,
,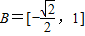
∴A∪B=[-1,1]
要使C⊆(A∪B),则
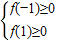
∴实数m的取值范围是m≥-1.
(2)
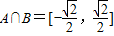
∵对任意x∈R,有f(1-x)=f(1+x)成立,
∴函数的对称轴为x=1
∴m=-4
∴f(x)=2x2-4x-1=2(x-1)2-3.
∵x∈(A∩B),
∴函数f(x)的值域为
 .
.(3)m∈[-1,1],x∈

∴f(x)的最小值为-1,最大值在端点处取得
∵


∴

点评:本题以集合为载体,考查函数值域,考查函数的最值,关键是集合的化简.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
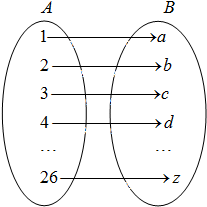 设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=
设f是由集合A={x|x∈N,且1≤x≤26}到B={a,b,c,…,z}(即26个英文字母按照字母表顺序排列)的映射,集合B中的任何一个元素在A中也只有唯一的元素与之对应,其对应法则如图所示(依次对齐);又知函数g(x)=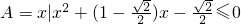 ,
,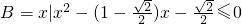 ,又设函数f(x)=2x2+mx-1.
,又设函数f(x)=2x2+mx-1.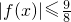 .
.