题目内容
6.(理)已知向量$\overrightarrow a=(m,1-n)$,$\overrightarrow b=(1,2)$,其中m>0,n>0,若$\overrightarrow a$∥$\overrightarrow b$,则$\frac{1}{m}+\frac{1}{n}$的最小值是3+2$\sqrt{2}$.分析 利用向量共线定理可得:n+2m=1,再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵$\overrightarrow a$∥$\overrightarrow b$,
∴1-n-2m=0,
化为n+2m=1,
又m>0,n>0,
则$\frac{1}{m}+\frac{1}{n}$=(n+2m)$(\frac{1}{m}+\frac{1}{n})$=3+$\frac{n}{m}$+$\frac{2m}{n}$≥3+2$\sqrt{\frac{n}{m}•\frac{2m}{n}}$=3+2$\sqrt{2}$,当且仅当n=$\sqrt{2}$m=$\sqrt{2}$-1时取等号.
故答案为:3+2$\sqrt{2}$.
点评 本题考查了向量共线定理、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
11.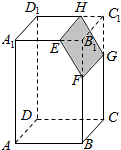 如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
 如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )| A. | EH∥FG | B. | 四边形EFGH是矩形 | ||
| C. | Ω是棱柱 | D. | 四边形EFGH可能为梯形 |
16.已知A={x|x-1>0},B={-2,-1,0,1,2},则A∩B=( )
| A. | {-2,-1} | B. | {2} | C. | {1,2} | D. | {0,1,2} |
 已知数列{an},观察程序框图,若k=5时,分别有S=25.
已知数列{an},观察程序框图,若k=5时,分别有S=25.