题目内容
15．已知函数f（x）为奇函数，当x＞0时，f（x）=-6x+2x，则f（f（-1））=-8．分析 由已知中函数f（x）为奇函数，可得f（-1）=-f（1），进而可得f（f（-1））的值．
解答 解：∵函数f（x）为奇函数，当x＞0时，f（x）=-6x+2x，
∴f（-1）=-f（1）=-（-6+2）=4，
∴f（f（-1））=f（4）=-24+16=-8，
故答案为：-8
点评 本题考查的知识点是函数奇偶性的性质，函数求值，难度中档．
练习册系列答案
相关题目
3．设$\overrightarrow{a}$=（cos2θ，sinθ），$\overrightarrow{b}$=（1，0），已知$\overrightarrow{a}$•$\overrightarrow{b}$=$\frac{7}{25}$，且$θ∈（\frac{π}{2}，π）$，则tanθ=（ ）
| A． | $-\frac{9}{16}$ | B． | $-\frac{3}{4}$ | C． | $\frac{3}{4}$ | D． | $±\frac{3}{4}$ |
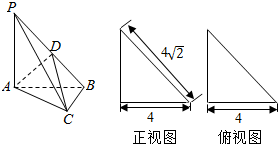在三棱锥P-ABC中，PA⊥平面ABC，AB⊥BC，D为侧棱PB的中点，它的正视图和侧视图如图所示，给出下列结论